Bài tập 5 trang 57 SGK Toán 8 Chân trời sáng tạo Tập 2
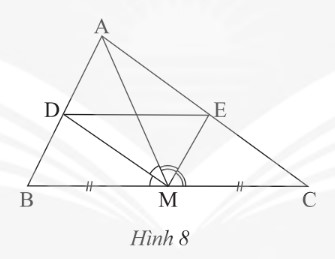
Cho tam giác \(ABC\) có trung tuyến \(AM\). Đường phân giác của góc \(AMB\) cắt AB tại D và đường phân giác của góc \(AMC\) cắt AC tại E (Hình 8). Chứng minh \(DE // BC\)?
Hướng dẫn giải chi tiết Bài 5
Xét tam giác \(ABM\) có MD là đường phân giác \(\widehat{AMB}\):
\(\Rightarrow \frac{DA}{DB}=\frac{MA}{MB}\)
Xét tam giác \(ACM\) có ME là đường phân giác góc \(\widehat{AMC}\):
\(\Rightarrow \frac{EA}{EB}=\frac{MA}{MC}\)
Mà \(MB = MC\), do đó: \(\frac{DA}{DB}=\frac{EA}{EC}\), theo định lí Thales đảo ta có: \(DE // BC\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


