Bài tập 5.3 trang 163 SBT Toán 8 Tập 1
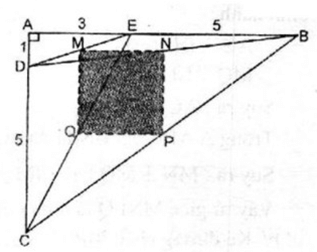
Cho tam giác vuông ABC, có hai cạnh góc vuông là AC = 6cm và AB = 8cm. Trên cạnh AC lấy điểm D sao cho CD = 5cm. Trên cạnh AB lấy điểm E sao cho EB = 5cm. Gọi M, N, P, Q tương ứng là trung điểm của các đoạn thẳng DE, DB, BC và CE. Tính diện tích của tứ giác MNPQ.
Hướng dẫn giải chi tiết
Trong ΔEDC ta có:
M là trung điểm của ED
Q là trung điểm của EC
nên MQ là đường trung bình của ΔEDC
⇒ MQ = \(\frac{1}{2}\) CD = 2,5 (cm) và MQ // CD
Trong ΔBDC ta có:
N là trung điểm của BD
P là trung điểm của BC
nên NP là đường trung bình của ΔBDC
⇒ NP = \(\frac{1}{2}\) CD = 2,5 (cm)
Trong ΔDEB ta có:
M là trung điểm của DE
N là trung điểm của DB
nên MN là đường trung bình của ΔDEB
⇒ MN = \(\frac{1}{2}\) BE = 2,5 (cm) và MN // BE
Trong ΔCEB ta có:
Q là trung điểm của CE
P là trung điểm của CB
nên QP là đường trung bình của ΔCEB
⇒ QP = \(\frac{1}{2}\) BE = 2,5 (cm)
Suy ra: MN = NP = PQ = QM (1)
MQ // CD hay MQ // AC
AC ⊥ AB (gt)
⇒ MQ ⊥ AB
MN // BE hay MN // AB
Suy ra: MQ ⊥ MN hay (QMN) = 900 (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình vuông
SMNPQ= MN2 = (2,5)2 = 6,25(cm2)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 5.1 trang 163 SBT Toán 8 Tập 1
Bài tập 5.2 trang 163 SBT Toán 8 Tập 1
Bài tập 42 trang 162 SBT Toán 8 Tập 1
Bài tập 43 trang 163 SBT Toán 8 Tập 1
Bài tập 44 trang 163 SBT Toán 8 Tập 1
Bài tập 45 trang 163 SBT Toán 8 Tập 1
Bài tập 46 trang 163 SBT Toán 8 Tập 1
Bài tập 5.1 trang 163 SBT Toán 8 Tập 1
-


Bài 42 trang 163 sách bài tập toán 8
bởi thu phương
 30/12/2019
Bài 42 (Sách bài tập - trang 162)
30/12/2019
Bài 42 (Sách bài tập - trang 162)Trong những hình thoi có chu vi bằng nhau, hãy tìm hình thoi có diện tích lớn nhất ?
Theo dõi (0) 1 Trả lời