Giải bài 3 tr 5 sách BT Toán lớp 8 Tập 2
Cho ba biểu thức \(5x - 3\), \({x^2} - 3x + 12\) và \(\left( {x + 1} \right)\left( {x - 3} \right)\)
a. Lập ba phương trình, mỗi phương trình có hai vế là hai trong ba biểu thức đã cho.
b. Hãy tính giá trị của các biểu thức đã cho khi x nhận tất cả các giá trị thuộc tập hợp M = {x ∈ ℤ | - 5 ≤ x ≤ 5 }, điền vào bảng sau rồi cho biết mỗi phương trình ở câu a. có những nghiệm nào trong tập hợp M:
|
x |
- 5 |
- 4 |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
5x – 3 |
|
|
|
|
|
|
|
|
|
|
|
|
\({x^2} - 3x + 12\) |
|
|
|
|
|
|
|
|
|
|
|
|
\(\left( {x + 1} \right)\left( {x - 3} \right)\) |
|
|
|
|
|
|
|
|
|
|
|
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) Sử dụng: Một phương trình với ẩn \(x\) có dạng \(A(x) = B(x)\), trong đó vế trái \(A(x)\) và vế phải \(B(x)\) là hai biểu thức của cùng một biến \(x.\)
b) Từ \(M=\{x ∈ ℤ | - 5 ≤ x ≤ 5\}\) suy ra: \(x \in \left\{ { - 5; - 4; - 3; - 2; - 1;0;1;2;3;4;5} \right\}\)
Thay các giá trị của \(x\) vào các biểu thức đã cho, từ bảng giá trị của các biểu thức ta tìm được nghiệm của các phương trình.
Lời giải chi tiết
a. (1): \(5x - 3 = {x^2} - 3x + 12\)
b. (2): \({x^2} - 3x + 12 = \left( {x + 1} \right)\left( {x -0 3} \right)\)
c. (3): \(5x - 3 = \left( {x + 1} \right)\left( {x - 3} \right)\
b. Ta có: x ∈ ℤ | - 5 ≤ x ≤ 5 suy ra:
\(x \in \left\{ { - 5; - 4; - 3; - 2; - 1;0;1;2;3;4;5} \right\}\)
|
x |
- 5 |
- 4 |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
5x – 3 |
- 28 |
- 23 |
- 18 |
- 13 |
- 8 |
- 3 |
2 |
7 |
12 |
17 |
22 |
|
\({x^2} - 3x + 12\) |
52 |
40 |
30 |
22 |
16 |
12 |
10 |
10 |
12 |
16 |
22 |
|
\(\left( {x + 1} \right)\left( {x - 3} \right)\) |
32 |
21 |
12 |
5 |
0 |
- 3 |
- 4 |
- 3 |
0 |
5 |
12 |
Phương trình (1) có nghiệm là x = 3 và x = 5
Phương trình (2) không có nghiệm
Phương trình (3) có nghiệm là x = 0
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Chọn khẳng định đúng
bởi nguyen bao anh
 15/01/2021
15/01/2021
A. Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm
B. Hai phương trình được gọi là tương đương nếu chúng có cùng số nghiệm
C. Hai phương trình được gọi là tương đương nếu chúng có chung một nghiệm
D. Hai phương trình được gọi là tương đương nếu chúng cùng điều kiện xác định
Theo dõi (0) 1 Trả lời -


Hai phương trình tương đương là hai phương trình có
bởi Bo Bo
 15/01/2021
15/01/2021
A. Một nghiệm giống nhau
B. Hai nghiệm giống nhau
C. Tập nghiệm giống nhau
D. Tập nghiệm khác nhau
Theo dõi (0) 1 Trả lời -


Giải các phương trình 2x +3=2017?
bởi Tu Vu Ba Tu
 16/08/2020
16/08/2020
Câu 1 : Giải các phương trình
a. 2x +3=2017
b. \(\dfrac{3x-1}{x-1}+ \dfrac{1}{x}=3\) ,
c. |5-x|=20
Theo dõi (0) 1 Trả lời -


Giải các phương trình sau:
bởi Bùi Khánh Linh
 23/07/2020
23/07/2020
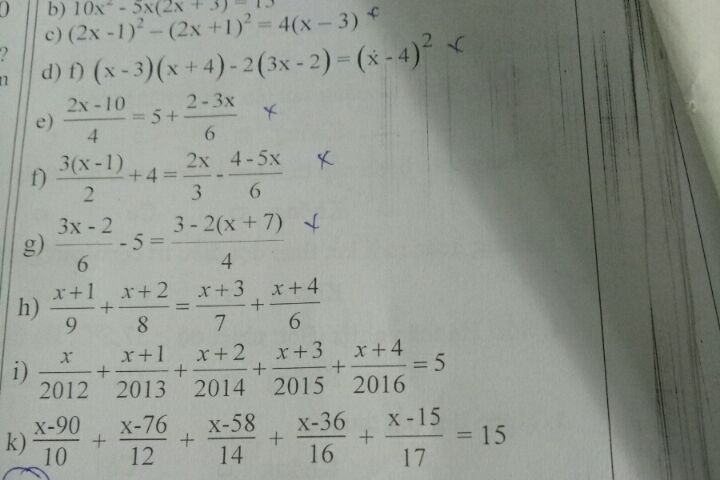 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -
ADMICRO


Thế nào là phương trình tương đương?
bởi Tú Hoàng
 19/06/2020
19/06/2020
Giải đề sau
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình x^2=-1?
bởi Phạm Văn Dô.
 05/06/2020
giải phương trìnhTheo dõi (0) 1 Trả lời
05/06/2020
giải phương trìnhTheo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm tập nghiệm của phương trình 2x = 8
bởi Nguyễn Lệ Diễm
 26/05/2020
Theo dõi (0) 2 Trả lời
26/05/2020
Theo dõi (0) 2 Trả lời -

 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


ập nghiệm của phương trình 3x - 6 = 0 là?
bởi Mai Bảo Khánh
 26/05/2020
26/05/2020
A. S = { 1 }
B. S = { 2 }
C. S = { - 2 }
D. S = { 1 }
Theo dõi (0) 2 Trả lời -


A. x = 1 và x( x - 1 ) = 0
B. x - 2 = 0 và 2x - 4 = 0
C. 5x = 0 và 2x - 1 = 0
D. x2 - 4 = 0 và 2x - 2 = 0
Theo dõi (0) 1 Trả lời -


x = - 4 là nghiệm của phương trình sau:
bởi Nguyễn Lệ Diễm
 26/05/2020
26/05/2020
A. - 2,5x + 1 = 11.
B. - 2,5x = - 10
C. 3x - 8 = 0
D. 3x - 1 = x + 7
Theo dõi (0) 1 Trả lời -


A. 2x = x + 1.
B. x + y = 3x.
C. 2a + b = 1.
D. xyz = xy.
Theo dõi (0) 1 Trả lời -


Chứng minh rằng các phương trình sau tương đương
bởi Nguyễn Thanh Trà
 26/05/2020
26/05/2020
2x = 6 và 1,5x = 4,5.
Theo dõi (0) 1 Trả lời


