Giải bài 102 tr 92 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo góc ABK, ACK.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Lời giải chi tiết
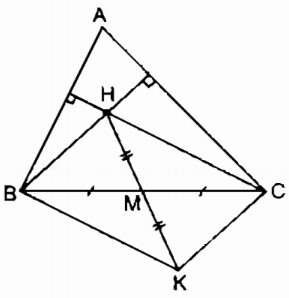
Ta có K là điểm đối xứng của H qua tâm M nên MK = MH
Xét tứ giác BHCK ta có:
BM = MC (gt)
MK = MH (chứng minh trên)
Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Suy ra: KB // CH, KC // BH
CH ⊥ AB (gt)
Suy ra: KB ⊥ AB nên \(\widehat {KBA} = {90^0}\)
BH ⊥ AC (gt)
Suy ra : CK ⊥ AC nên \(\widehat {KCA} = {90^0}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


GIúp mình với
bởi .......XxX Gamers
 28/07/2017
28/07/2017
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với điểm D qua A, gọi F là điểm đối xứng với điểm D qua C. Chứng minh rằng điểm E đối xứng với điểm F qua điểm B.
Theo dõi (0) 2 Trả lời





