Bài tập 3.13 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy của nó?
Hướng dẫn giải chi tiết Bài tập 3.13
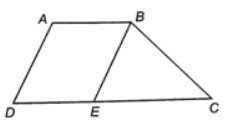
Xét hình thang ABCD với hai đáy AB và CD. Giả sử AB < CD.
Kẻ đường thẳng đi qua B song song với AD, cắt CD tại E.
Xét tứ giác ABED có: AB // DE và AD // BE
Do đó ABED là hình bình hành nên AB = DE và AD = BE.
Do AB < CD nên E nằm giữa C và D, do đó EC = DC – DE hay EC = DC ‒ AB. (1)
Trong tam giác BEC có: BE + BC > EC (bất đẳng thức trong tam giác)
Mà AD = BE nên AD + BC > EC (2)
Từ (1), (2) suy ra AD + BC > DC – AB.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài 3.18 trang 61 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài tập 3.12 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.14 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.15 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.16 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.17 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.18 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.19 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


