Bài 1 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(A\left( { - 2;0} \right);B\left( {3;0} \right);C\left( {4;0} \right)\).
a) Em nhận xét gì về các điểm \(A;B;C\)?
b) Em hãy cho biết một điểm bất kì trên trục hoành có tung độ bằng bao nhiêu?
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải:
- Điểm \(A\left( {{x_0};{y_0}} \right)\) thì hoành độ là \({x_0}\) và tung độ là \({y_0}\).
- Điểm \(B\left( {0;b} \right)\) nằm trên trục tung, tung độ là \(b\).
- Điểm \(C\left( {c;0} \right)\) nằm trên trục hoành, hoành độ là \(c\).
Lời giải chi tiết:
a)
Điểm \(A\left( { - 2;0} \right) \Rightarrow \) hoành độ là -2 và tung độ là 0.
Điểm \(B\left( {3;0} \right) \Rightarrow \) hoành độ là 3 và tung độ là 0.
Điểm \(C\left( {4;0} \right) \Rightarrow \) hoành độ là 4 và tung độ là 0.
Biểu diễn ba điểm \(A;B;C\) trên hệ trục tọa độ ta được
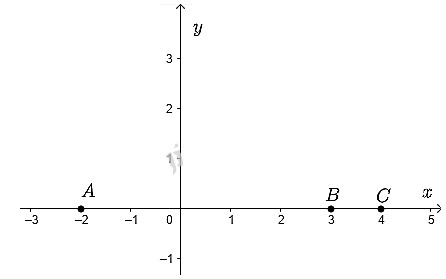
Nhận xét: Cả ba điểm \(A;B;C\) đều nằm trên trục hoành.
b) Từ ví dụ ở câu a ta thấy tất cả các điểm nằm trên trục hoành đều có tung độ bằng 0.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Thực hành 3 trang 13 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 3 trang 13 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài 2 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài 3 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài 4 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài 5 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài 6 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài 7 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài 8 trang 14 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


