Bài 4 trang 78 SGK Toán 8 Tập 2 Cánh diều
Cho tam giác ABC và điểm O nằm trong tam giác. Các điểm M, N, P lần lượt thuộc các tia OA, OB, OC sao cho \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}} = \frac{{OC}}{{OP}} = \frac{2}{3}\). Chứng minh \(\Delta ABC \backsim\Delta MNP\)?
Hướng dẫn giải chi tiết Bài 4
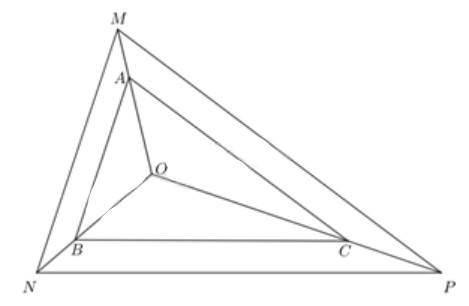
Xét tam giác MON có: \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}} = \frac{2}{3}\) nên \(AB//MN\) (Định lý Thales đảo)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{2}{3}\) (Hệ quả của định lý Thales)
Chứng minh tương tự ta được: \(\frac{{BC}}{{NP}} = \frac{2}{3};\,\,\frac{{AC}}{{MP}} = \frac{2}{3}\)
\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{AC}}{{MP}}\)
\( \Rightarrow \Delta ABC \backsim\Delta MNP\) (c - c - c)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





