Bài 4 trang 69 SGK Toán 8 Tập 2 Cánh diều
Cho hình thoi ABCD (Hình 44). Điểm M thuộc cạnh AB thỏa mãn \(AB = 3AM\). Hai đoạn thẳng AC và DM cắt nhau tại N. Chứng minh \(ND = 3MN\)?
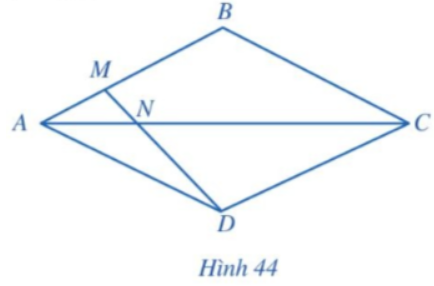
Hướng dẫn giải chi tiết Bài 4
Gọi giao điểm hai đường chéo của hình thoi là O.
Khi đó AC vuông góc với BD tại O.
Vì ABCD là hình thoi nên \(AB = AD\) hay tam giác ABD cân tại A.
Khi đó AO vừa là đường cao, vừa là phân giác của tam giác ABD.
Xét tam giác AMD với AN là đường phân giác, ta có:
\(\frac{{ND}}{{NM}} = \frac{{AD}}{{AM}}\,\,\left( 1 \right)\) (Tính chất đường phân giác)
Mà \(AB = 3AM \Rightarrow \frac{{AB}}{{AM}} = 3 \Rightarrow \frac{{AD}}{{AM}} = 3\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(\frac{{ND}}{{NM}} = 3 \Rightarrow ND = 3DM\).
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





