Giải Câu hỏi 5 trang 47 SBT Toán 7 Kết nối tri thức tập 1 - KNTT

Phương pháp giải:

Nếu OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\) 

Hai góc đối đỉnh thì bằng nhau

Lời giải chi tiết:

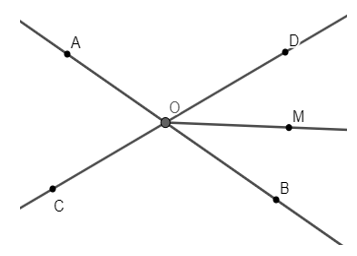
Vì OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\) nên \(\widehat{BOD}=2. \widehat{BOM}=2.30^0=60^0\)

Ta có: \(\widehat{AOC}=\widehat{BOD}\) ( 2 góc đối đỉnh)

Do đó, \(\widehat{AOC}=60^0\)

Chọn B

-- Mod Toán 7 HỌC247