Giải bài 84 trang 93 SBT Toán 7 Cánh diều tập 2 - CD

Phương pháp giải

- Chứng minh: \(\widehat {AGE} = \widehat {AGD}\) nên GA là tia phân giác góc DGE.

Chứng minh: \(\widehat {BGM} = \widehat {CGM}\) nên GM là tia phân giác góc BGC.

Chứng minh: \(\widehat {AME} = \widehat {AMD}\) nên MA là tia phân giác góc EMD.

- Cho EG là tia phân giác của góc DEM chứng minh tam giác ABC đều (AB = AB = BC)

Lời giải chi tiết

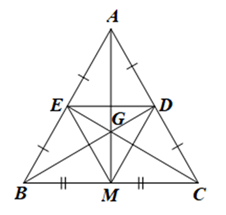
a)• Vì tam giác ABC cân tại A nên AB = AC, \(\widehat {ACB} = \widehat {ABC}\).

Vì E là trung điểm của AB nên AE = EB = \(\frac{1}{2}\)AB.

Vì D là trung điểm của AC nên AD = CD = \(\frac{1}{2}\) AC.

Mà AB = AC nên AE = EB = AD = CD.

Tam giác ABC có hai trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Do đó đường trung tuyến AM của tam giác ABC cũng đi qua G.

Hay ba điểm A, G, M thẳng hàng.

Xét ∆ABM và ∆ACM có:

AB = AC (chứng minh trên),

AM là cạnh chung,

MB = MC (do M là trung điểm của BC).

Do đó ∆ABM = ∆ACM (c.c.c)

Suy ra \(\widehat {BAM} = \widehat {CAM}\) (hai góc tương ứng)

Xét ∆AEG và ∆ADG có:

AE = AD (chứng minh trên),

\(\widehat {EAG} = \widehat {DAG}\) (do \(\widehat {BAM} = \widehat {CAM}\)),

AG là cạnh chung

Do đó ∆AEG = ∆ADG (c.g.c).

Suy ra \(\widehat {AGE} = \widehat {AGD}\) (hai góc tương ứng).

Do vậy GA là tia phân giác của góc DGE.

• Ta có \(\widehat {BGM} = \widehat {AGD},\widehat {CGM} = \widehat {AGE}\) các cặp góc đối đỉnh)

Mà \(\widehat {AGE} = \widehat {AGD}\)

Nên \(\widehat {BGM} = \widehat {CGM}\)

Do đó GM là tia phân giác của góc BGC.

• Xét ∆AME và ∆AMD có:

AE = AD (chứng minh trên),

\(\widehat {E{\rm{A}}M} = \widehat {DAM}\) (do \(\widehat {BAM} = \widehat {CAM}\)),

AM là cạnh chung,

Do đó ∆AME = ∆AMD (c.g.c).

Suy ra \(\widehat {AME} = \widehat {AMD}\) (hai góc tương ứng)

Nên MA là tia phân giác của góc EMD.

Vậy GA, GM, MA lần lượt là tia phân giác của các góc DGE, BGC, EMD.

b) • Xét ∆ABC có \(\widehat {ABC} + \widehat {ACB} + \widehat {CAB} = 180^\circ \) (tổng ba góc của một tam giác)

Mà \(\widehat {ABC} = \widehat {ACB}\) nên \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ  - \widehat {BAC}}}{2}\) 

Ta có AE = AD (chứng minh câu a)

Nên tam giác AED cân tại A

Suy ra \(\widehat {AE{\rm{D}}} = \widehat {ADE}\)

Xét ∆ADE có \(\widehat {ADE} + \widehat {AE{\rm{D}}} + \widehat {DA{\rm{E}}} = 180^\circ \) (tổng ba góc của một tam giác)

Mà \(\widehat {AE{\rm{D}}} = \widehat {ADE}\) nên \(\widehat {AED} = \widehat {ADE} = \frac{{180^\circ  - \widehat {BAC}}}{2}\)

Từ (1) và (2) suy ra \(\widehat {AED} = \widehat {ABC}\)

Mà hai góc này ở vị trí đồng vị

Do đó ED // BC.

Nên \(\widehat {DEC} = \widehat {ECM}\) (hai góc so le trong)

• Để EG là tia phân giác của góc DEM thì \(\widehat {DEC} = \widehat {CEM}\)

Suy ra \(\widehat {ECM} = \widehat {CEM}\) nên tam giác MEC cân tại M.

Do đó ME = MC

Mặt khác, MB = MC nên ME = MB = MC.

Suy ra tam giác EMB cân tại M nên \(\widehat {MEB} = \widehat {MBE}\).

• Xét ∆EBC có \(\widehat {BEC} + \widehat {BCE} + \widehat {EBC} = 180^\circ \) (tổng ba góc của một tam giác)

Hay \(\widehat {BEC} + \widehat {MCE} + \widehat {MBE} = 180^\circ \)

Mà \(\widehat {MEC} = \widehat {MCE}\) và \(\widehat {MEB} = \widehat {MBE}\)

Nên \(\widehat {BEC} + \widehat {MEC} + \widehat {MEB} = 180^\circ \) hay \(\widehat {BEC} + \widehat {BEC} = 180^\circ \)

Suy ra \(2\widehat {BEC} = 180^\circ \)

Do đó \(\widehat {BEC} = \frac{{180^\circ }}{2} = 90^\circ \) nên \(\widehat {AEC} = 90^\circ .\)

• Xét ∆BEC và ∆AEC có:

\(\widehat {BEC} = \widehat {AEC}\) (cùng bằng 90°),

EC là cạnh chung,

BE = AE (chứng minh câu a)

Do đó ∆BEC = ∆AEC (hai cạnh góc vuông).

Suy ra BC = AC.

Mà AB = AC (chứng minh câu a).

Do đó AB = BC = AC nên tam giác ABC là tam giác đều.

Vậy điều kiện để EG là tia phân giác của góc DEM là tam giác ABC là tam giác đều.

-- Mod Toán 7 HỌC247