Giải bài 7.29 trang 34 SBT Toán 7 Kết nối tri thức tập 2 - KNTT

Phương pháp giải:

Đặt phép tính chia A cho B để tìm thương Q và số dư R

Lời giải chi tiết:

\(A = 3{x^4} + {x^3} + 6x - 5;B = {x^2} + 1\)

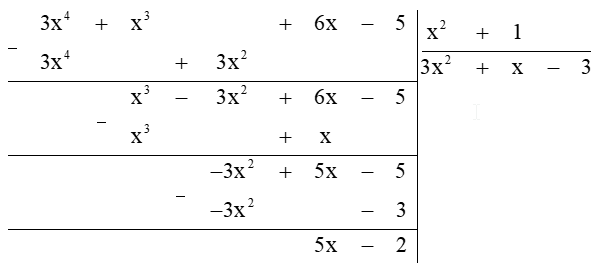
Vậy chia A cho B ta được thương là \(Q = 3{x^2} + x - 3\) và số dư \(R = 5x - 2\).

-- Mod Toán 7 HỌC247