Giải bài 4.30 trang 61 SBT Toán 7 Kết nối tri thức tập 1
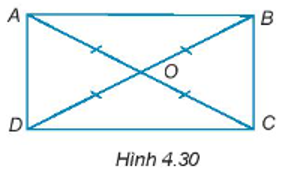
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OB = OC = OD như Hình 4.30. Chứng minh ABCD là hình chữ nhật.
Hướng dẫn giải chi tiết
Phương pháp giải:
Dựa vào đặc điểm của hình chữ nhật.
Lời giải chi tiết:
Xét ∆OAB và ∆OCD ta có:
OA = OC (giả thiết)
\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
OB = OD (giả thiết)
Do đó, ∆OAB = ∆OCD (c – g – c). \
Suy ra AB = DC và \(\widehat {BAO} = \widehat {COD}\) hay \(\widehat {BAC} = \widehat {ACD}\)
Mà hai góc này ở vị trí so le trong, do đó AB // DC (1).
Xét ∆OAD và ∆OCB ta có:
OA = OC (giả thiết)
\(\widehat {AOD} = \widehat {BOC}\) (hai góc đối đỉnh)
OD = OB (giả thiết)
Do đó, ∆OAD = ∆OCB (c – g – c).
Suy ra AD = BC và \(\widehat {OAD} = \widehat {OCB}\) hay \(\widehat {CAD} = \widehat {ACB}\)
Mà hai góc này ở vị trí so le trong nên AD // BC (2).
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành.
Ta có: OA = OC = OB = OD, AC = OA + OC, BD = OB + OD.
Do đó, AC = BD.
Xét tam giác ABD và tam giác DCA có:
AB = DC (chứng minh trên)
AD: cạnh chung
BD = AC (chứng minh trên)
Do đó, ∆ABD = ∆DCA (c – c – c).
Suy ra \(\widehat {BAD} = \widehat {CDA}\)
Lại có: \(\widehat {BAD} + \widehat {CDA}\) = 180° (do AB // DC, hai góc ở vị trí trong cùng phía)
Do đó: \(\widehat {BAD} = \widehat {CDA}\) =180°/2=90°.
Vậy hình bình hành ABCD có một góc vuông nên nó là hình chữ nhật.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


