Giải bài 2 trang 55 SBT Toán 7 Chân trời sáng tạo tập 2
Cho góc xOy bằng \({45^o}\) và điểm M nàm trong góc xOy. Vẽ điểm N sao cho Ox là trung trực của MN, vẽ điểm P sao cho Oy là đường trung trực của MP.
a) Chứng minh ON = OP.
b) Tính số đo góc NOP
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
Sử dụng tính chất của đường trung trực để chứng minh ON = OP
Lời giải chi tiết
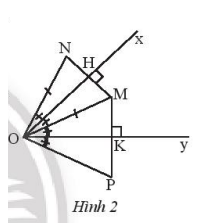
a) Ta có Ox là đường trung trực của MN, suy ra OM = ON
Ta có Oy là đường trung trực của MP, suy ra OM = OP.
Vậy ON = OP.
b) Gọi H và K lần lượt là trung điểm của MN và MP nên HM = HN ; KM = KP
Ta có: \(\Delta OHM = \Delta OHN\) ( vì OH chung, OM = ON, HM = HN)
\(\Delta OKM = \Delta OKP\) (vì OK chung, OM = OP, KM = KP)
Suy ra: \(\widehat {NOP} = \widehat {NOM} + \widehat {MOP} = 2\left( {\widehat {xOM} + \widehat {MOy}} \right) = 2\widehat {xOy} = {2.45^o} = {90^o}\)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





