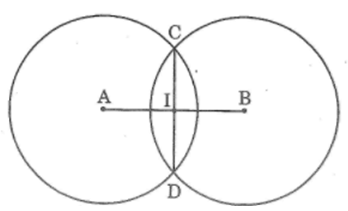
Bài tập 38 trang 93 SBT Toán 6 Tập 2

Bạn Lan đi xe đạp từ nhà đến trường , đoạn đường dài 2,826 km . Bánh xe có đường kính 60 cm . Hỏi bánh xe quay hết bao nhiêu vòng ?

Bài 1: Cho đường tròn (O;R),đượng kính AB,qua A và B vẽ lần lượt hai tiếp tuyến d và d' với đường tròn (O) , một đường thẳng qua O cắt d ở M, cắt d' ở P.Từ O vẽ một đường vuông góc với MP và cắt d' tại N

a) Cm ON=OP và △NMP cân

b)Cm AN.BN=R²

c) Cm AB là tiếp tuyến của đường tròn,đường kính MN

d)M di chuyển trên đường thẳng d,tìm vị trí của M để S_{tứ giác AMNB} là nhỏ nhất

câu 1 ; cho đường tròn tâm (O;R) đường kính AB và điểm M nằn trên đường tròn sao cho MAB= 60 độ . kẻ dây MN vuông góc AB tại H
a, cm: AM và AN LÀ các tiếp tuyến của đường tron (M;BM)
b, chứng minh : NM^2=4AH.HB
c, cm : th BNM là tg đều và điểm O là trọng tâm của nó
d, tia OM cắt đường tròn (O) tại E tia BM cắt (B)tại E cm : ba điểm N,E,F thẳng hàng

1.CMR: tam giác ABC có D,E lần lượt thuộc các tia AB, AC thì \(\dfrac{\Delta ADE}{\Delta ACB}\)= \(\dfrac{AD}{AB}\cdot\dfrac{AE}{AC}\)

2. Nhờ các bạn chứng minh định lí Stewart hộ mình!

3.Cho tam giác ABC, AM là trung tuyến. CMR: \(AM^2=\dfrac{2\left(AB^2+AC^2\right)-BC^2}{4}\)

Cho đường tròn tâm O đường kính AB , qua trung điểm I của OA. kẻ dây MN vuông góc với AB , từ O ker OP vuông góc BM(P\(\in\)BM). CM rằng:

a) Tứ giác AMON là hình thoi

b) \(IM^2=IA.IB\)

c) BA điểm P,O,N thẳng hàng

Từ điểm M nằm ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.

a) CMR: MT² = MA.MB

b) Biết MT=20cm và cát tuyến dài nhất cùng xuất phát từ điểm M bằng 50cm. Tính bán kính của đường tròn

Cho đường tròn tâm O đường kính AB, M là điểm chính giữa cung AB, K là 1 điểm bất kì trên cung nhỏ BM. Gọi H là chân đường vuông góc của M xuống AK

a) CM: AOHM nội tiếp

b) tam giác MHK là tam giác gì? Vì sao ?

c) CM: OH là phân giác góc MOK

d) Gọi P là hình chiếu của K lên AB. Xác định vị trí điểm K để chu vi tam giác OPK lớn nhất

khi giảm bán kính của hình tròn đi 15% thì chu vi hình tròn đó sẽ giảm :.............%

Cho hình thoi ABCD.Đường trung trực của cạnh AB cắt BD tại E và cắt AC tại F .Chứng minh E,F lần lượt là tâm của đường tròn ngoại tiếp các tam giác ABC và ABD.

Cho hình thang ABCD ( AB//CD , AB < CD) có góc C= D= 600, AB= 3cm, CD=2AD. CM 4 điểm A, B, C ,D cùng thuộc một đường tròn . Xác định tâm và tính bán kính của đường tròn này.

Cho đg tròn (O,R) từ 1 điểm A trên O kẻ tiếp tuyến d vs (O). Trên đg thẳng d lấy M bất kì(M khác A), kẻ cát tuyến MNP và gọi K là trung điểm NP, kẻ tiếp tuyến MB( B là tiếp điểm). Kẻ AC vuông góc MB, BD vuông góc MÀ, gọi H là giao của AC và BD, I là giao OM và AB

a)CM: AMBO nội tiếp đường tròn

b)CM: 5 điểm O,K,A,M,B cùng nằm trên 1 đg tròn

c)CM: OI.OM=R^2 ; OI.IM=IA^2

d)CM: 3 điểm O,H,M thẳng hàng

Giúp mình nhé

bài 1: Cho đường tròn tâm O bán kính r đường kính ab. Vẽđường thằng d tiếp xúc với đường tròn (O) tại A. Trên d lấy điểm P, kẻ tiếp tuyến PC với đường tròn (O) (C là tiếp điểm) ( cần hình vẽ )

a) CM tứ giác APCO nội tiếp

b) CM góc AOP bằng góc ABC

ΔABC ( AB <AC ) có 3 góc nhọn. Đường tròn (O; \(\dfrac{BC}{2}\)) cắt AC, AB lần lượt tại E, F. BE cắt CF tại H; AH cắt BC tại D.

a, C/m: AH . AD = AE . AC

b, C/m: Tứ giác EFDO nội tiếp.

c, Trên tia đối của tia DE, lấy điểm I sao cho: DI = DF. Tính góc BIC.

Mình làm a, và b, rồi ạ! Mog các bạn chỉ cho mình câu c, ạ ! Cảm ơn ạ !