Để học tốt bài Số đo góc. Các góc đặc biệt, HỌC247 xin mời các em cùng tham khảo bài giảng dưới đây bao gồm các kiến thức được trình bày cụ thể và chi tiết, cùng với các dạng bài tập minh họa giúp các em dễ dàng nắm vững được trọng tâm bài học.
Tóm tắt lý thuyết
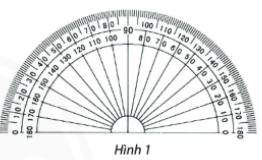
1.1. Thước đo góc
Độ là đơn vị đo góc
Ta gọi tâm của nửa hình tròn này là tâm của thước
1.2. Cách đo góc. Số đo góc
Dùng thước đo góc, xác định số đo của góc xOy cho trước.
- Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.
- Bước 2: xoay thước sao cho một cạnh của góc (chẳng hạn cạnh Oy) đi qua vạch O của thước và thước chồng lên phần trong của góc như Hình 2.
- Bước 3: Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.
Nhận xét:
- Mỗi góc có một số đo. Số đo của góc bẹt là \({180^0}\)
- Số đo của mỗi góc không vượt quá \({180^0}\)
1.3. So sánh hai góc
Ta so sánh hai góc bằng cách so sánh số đo của chúng.
- Hai góc bằng nhau nếu số đo của chúng bằng nhau.
Ví dụ: \(\widehat xOy = \widehat zIt\)
- Trong hai góc, góc nào có số đo lớn hơn (bé hơn) thì góc đó lớn hơn (bé hơn).
Ví dụ: \(\widehat mOn > \widehat pIq\) hoặc \(\widehat pIq < \widehat mOn\)
1.4. Các góc đặc biệt
- Góc có số đo bằng 900 là góc vuông.
- Góc có số đo nhỏ hơn 900 là góc nhọn.
- Góc có số đo lớn hơn 900 nhưng nhỏ hơn 1800 là góc tù
Bài tập minh họa
Cho hình sau có điểm I là trung điểm của đoạn thẳng BC. Hãy đo để kiểm tra xem hai góc BAI và IAC có bằng nhau không?
Hướng dẫn giải
Dùng thước đo độ để tìm số đo hai góc.
Góc nào có số đo lớn hơn thì lớn hơn.
Hai góc có số đo bằng nhau thì bằng nhau.
Ta có:
\(\eqalign{& \widehat {BAI} = {20^o} \cr & \widehat {IAC} = {45^o} \cr} \)
Suy ra \(\widehat {BAI} < \widehat {IAC}\).
Luyện tập Bài 7 Chương 8 Toán 6 CTST
Qua bài giảng này giúp các em biết được:
- Cách đo góc. Số đo góc
- So sánh hai góc.
- Các góc đặc biệt.
3.1. Bài tập tự luận về Số đo góc. Các góc đặc biệt
Câu 1: Hãy cho biết mỗi câu sau đây là đúng hay sai?
a) Góc có số đo \({75^0}\) là góc tù
b) Góc có số đo \({180^0}\) là góc vuông
c) Một góc không phải là góc tù thì phải là góc nhọn
d) Một góc bé hơn góc bẹt thì phải là góc tù
Câu 2: Cho hình
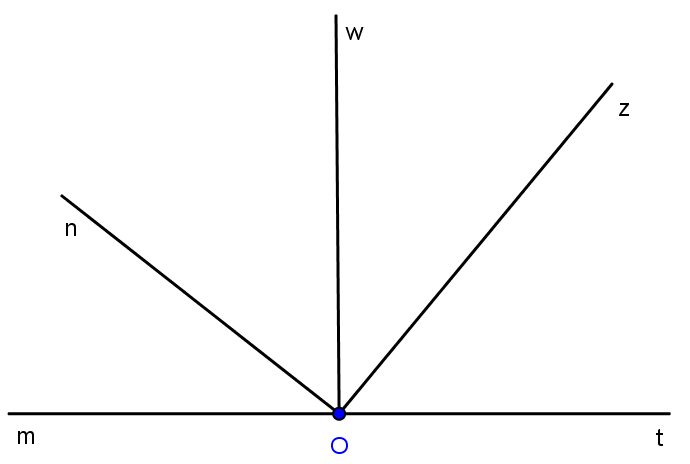
a) Hãy đọc tên các góc đỉnh O có trong hình đó.
b) Cho biết số đo của góc nhọn đỉnh O, một cạnh là Ot có trong hình đó.
c) Hãy đo và cho biết tên của các góc vuông đỉnh O có trong hình đó.
d) Cho biết số đo của các góc tù đỉnh O có trong hình đó.
3.2. Bài tập trắc nghiệm về Số đo góc. Các góc đặc biệt
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 6 Chân trời sáng tạo Chương 8 Bài 7 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
Câu 1:
Chọn phát biểu đúng.
- A. Góc có số đo 1200 là góc vuông
- B. Góc có số đo 800 là góc tù
- C. Góc có số đo 1000 là góc nhọn
- D. Góc có số đo 1500 là góc tù
-
Câu 2:
Chọn câu sai.
- A. Góc vuông là góc có số đo bằng 900
- B. Góc có số đo lớn hơn 00 và nhỏ hơn 900 là góc nhọn
- C. Góc tù là góc có số đo lớn hơn 900 và nhỏ hơn 1800
- D. Góc có số đo nhỏ hơn 1800 là góc tù
-
- A. 3
- B. 4
- C. 5
- D. 6
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.3 Bài tập SGK về Số đo góc. Các góc đặc biệt
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 6 Chân trời sáng tạo Chương 8 Bài 7 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 6 tập 1
Hoạt động khám phá 1 trang 89 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Thực hành 1 trang 89 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 90 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 2 trang 91 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 91 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 91 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 91 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 91 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 101 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 101 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 101 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 101 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 101 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 102 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 7 trang 102 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 8 trang 102 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Hỏi đáp Bài 7 Chương 8 Toán 6 CTST
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 6 HỌC247


.PNG)
.PNG)
.PNG)
.PNG)
