Để làm quen với kiến thức toán lớp 6 đầu tiên ta sẽ ôn tập và hệ thống hóa nội dung về số tự nhiên. Đầu tiên ta sẽ làm quen với tập hợp và các kí hiệu tập hợp qua bài học đầu tiên là Tập hợp, Phần tử của tập hợp. Nội dung bài học sẽ giúp các em khái niệm tập hợp qua các ví dụ về tập hợp thường gặp trong toán học và trong đời sống, biết một số đối tượng thuộc hay không thuộc một tập hợp cho trước và viết một tập hợp theo diễn đạt bằng lời của bài toán, biết sử dung kí hiệu.
Tóm tắt lý thuyết
1.1. Làm quen với tập hợp
- Khái niệm tập hợp thường gặp trong toán học và trong đời sống
Ví dụ:
Em hãy viết vào vở
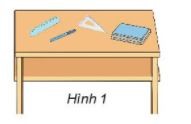
- Tên các đồ vật trên bàn Hình 1
- Tên các bạn trong tổ của em
- Các số tự nhiên vừa lớn hơn 3 vừa nhỏ hơn 12
Hướng dẫn giải
- Tên các đồ vật trên bàn ở hình 1: Thước thẳng, thước êke, cây bút, quyển vở.
- Tên các bạn trong tổ: các em tự viết các tên các bạn trong tổ.
- Các số tự nhiên vừa lớn hơn 3 vừa nhỏ hơn 12 là các số: 4, 5, 6, 7, 8, 9, 10, 11, 12.
1.2. Các kí hiệu tập hợp
Người ta thường dùng các chữ in hoa A; B; C,….để kí hiệu tạp hợp, các chữ in thường a, b, c,…để kí hiệu phần tử của tập hợp
- Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu phẩy “,” hoặc dấu chấm phẩy “;” (đối với trường hợp các phần tử là số). Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
- Phần tử x thuộc tập hợp A được kí hiệu là x ∈ A, đọc là “x thuộc A”. Phần tử y không thuộc tập hợp A được kí hiệu là y ∉ A, đọc là y không thuộc A.
Ví dụ:
a) Gọi A là tập hợp các số tự nhiên nhỏ hơn 6. Ta có: A = {0; 1; 2; 3; 4; 5}.
Ta cũng có thể viết A = {1; 5; 2; 4; 0; 3},…..
Mỗi số 0; 1; 2; 3; 4; 5 là một phần tử của tập hợp A. Số 8 không là phần tử của tập hợp A (8 không thuộc A)
Ta viết: 0 ∈ A; 1 ∈ A; …;5 ∈A; 8 ∉ A
b) Gọi B là tập hợp các chữ cái có mặt trong từ “nhiên”
Ta có: B = {n, h, i, ê} hoặc B = {h; i; ê; n}; n ∈ B; i ∈ B; k ∉ B
1.3. Cách cho tập hợp
Có hai cách cho một tập hợp:
- Liệt kê các phần tử của tập hợp
- Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp3
Ví dụ:
a) Viết tập hợp A các chữ cái có trong chữ “TRƯỜNG HỌC” bằng cách liệt kê các phần tử.
b) Viết tập hợp B các số tự nhiên lớn hơn 5 và nhỏ hơn 10 bằng hai cách.
Hứớng dẫn giải
a) A = {T, R, U, O, N, G, H, C}
b) Cách 1: B = {6; 7; 8; 9}
Cách 2: B = {x ∈ N | 5 < x < 10}
Bài tập minh họa
Câu 1: Gọi M là tập hợp các chữ cái Tiếng Việt có mặt trong từ "gia đình"
a) Hãy viết tập hợp M bằng cách liệt kê các phần tử
b) Các khẳng định sau đây đúng hay sai
a ∈ M
o ∈ M
b ∉ M
e ∈ M
Hướng dẫn giải
a) M = {g, i, a, đ, i, n, h}
b) a ∈ M => Đúng
o ∈ M => Sai
b ∉ M => Đúng
e ∈ M => Sai
Câu 2: Cho tập hợp E = {0; 2; 4;6; 8). Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp E và viết tập hợp E theo cách này.
b) Cho tập hợp P = {x | x là số tự nhiên và 10 < x < 20). Hãy viết tập hợp P theo cách liệt kê tất cả các phần tử.
Hướng dẫn giải
a) E = {x | x là số tự nhiên chẵn, và x ≤ 8}
b) P = {11, 12, 13, 14, 15, 16, 17, 18, 19}
Câu 3: Cho tập hợp A gồm các số tự nhiên vừa lớn hơn 7 vừa nhỏ hơn 15.
a) Hãy viết tập hợp A theo cách liệt kê các phần tử.
b) Kiểm tra xem trong những số 10; 13; 16; 19, số nào là phần tử thuộc tập hợp A, số nào không thuộc tập hợp A.
c) Gọi B là tập hợp các số chẵn thuộc tập hợp A. Hãy viết tập hợp B theo hai cách
Hướng dẫn giải
a) A = {8, 9, 10, 11, 12, 13, 14, 15}
b) 10 ∈ A; 13 ∈ A
16 ∉ A, 19 ∉ A
c) Cách 1: B = {8, 10, 12, 14}
Cách 2: B = { x | x là số tự nhiên chẵn, và 7 < x < 15}
Luyện tập Bài 1 Chương 1 Toán 6 CTST
Qua bài giảng này giúp các em nắm được các nội dung như sau:
- Biết khái niệm tập hợp qua các ví dụ về tập hợp thường gặp trong toán học và trong đời sống.
- Biết một số đối tượng thuộc hay không thuộc một tập hợp cho trước.
- Viết một tập hợp theo diễn đạt bằng lời của bài toán, biết sử dụng kí hiệu .
3.1. Bài tập tự luận về Tập hợp, Phần tử của tập hợp
Câu 1: Cho tập hợp A là các chữ cái trong cụm từ “Số học Toán 6”
a. Hãy liệt kê các phần tử của tập hợp A.
b. Điền kí hiệu thích hợp vào ô vuông
o [ ] A; a [ ] A; b [ ] A
Câu 2: Cho tập hợp A = {10; 20;30;x; y; z}
a/ Hãy chỉ rõ các tập hợp con của A có 1 phần tử.
b/ Hãy chỉ rõ các tập hợp con của A có 2 phần tử.
c/ Tập hợp B = {x, y, z} có phải là tập hợp con của A không?
Câu 3: Cho tập hợp B = {x, y, z, t}. Hỏi tập hợp B có tất cả bao nhiêu tập hợp con?
3.2. Bài tập trắc nghiệm về Tập hợp, Phần tử của tập hợp
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 6 Chân trời sáng tạo Chương 1 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. A = {6;7;8;9}.
- B. A = {5;6;7;8;9}.
- C. A = {6;7;8;9;10}.
- D. A = {6;7;8}.
-
- A. 4
- B. 5
- C. 6
- D. 7
-
- A. 9
- B. 6
- C. 8
- D. 7
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.3. Bài tập SGK về Tập hợp, Phần tử của tập hợp
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 6 Chân trời sáng tạo Chương 1 Bài 1 . Thông qua các bài tập này sẽ giúp các em nắm được các phương pháp giải bài tập Toán 6 và ôn lại bài hiệu quả.
Thực hành 1 trang 8 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 8 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 8 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 8 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 9 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 9 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 9 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 9 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 7 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 7 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 7 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 7 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 8 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Hỏi đáp Bài 1 Chương 1 Toán 6 CTST
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 6 HỌC247





