Hoạt động khám phá 2 trang 27 SGK Toán 11 Chân trời sáng tạo tập 2
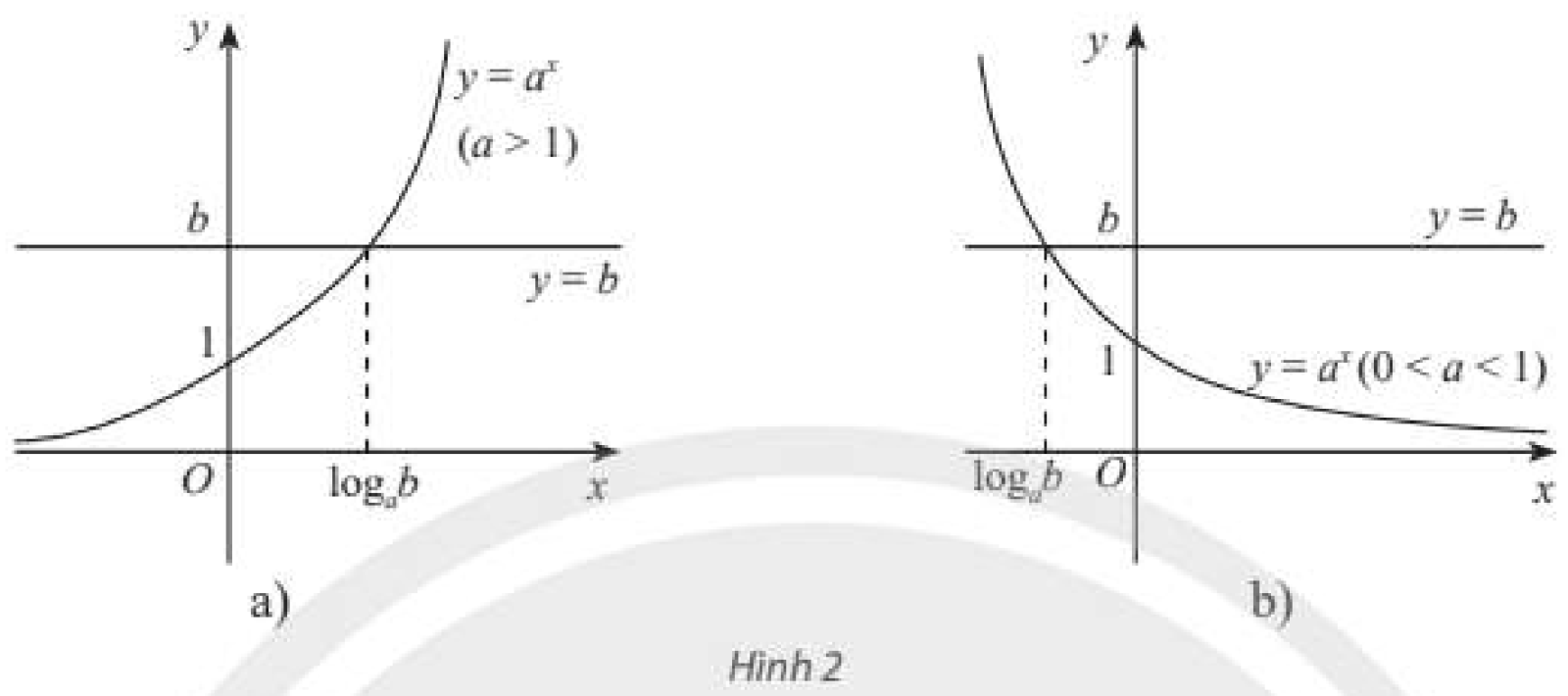
Cho đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) như Hình 2a (với \(a > 0\)) hay Hình 2b (với \(0 < a < 1\)). Từ đây, hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({a^x} = b\) trong hai trường hợp \(b > 0\) và \(b \le 0\).
Hướng dẫn giải chi tiết Hoạt động khám phá 2
Phương pháp giải:
Quan sát đồ thị, dựa vào số điểm chung của đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\).
Lời giải chi tiết:
Khi \(b > 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) cắt nhau tại một điểm duy nhất. Khi đó phương trình \({a^x} = b\) có nghiệm duy nhất \(x = {\log _a}b\).
Khi \(b \le 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) không có điểm chung. Khi đó phương trình \({a^x} = b\) vô nghiệm.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Hoạt động khám phá 1 trang 26 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 1 trang 28 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 1 trang 28 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 3 trang 28 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 4 trang 29 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 30 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 5 trang 30 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 3 trang 31 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 6 trang 31 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 32 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 2 trang 32 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 32 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 33 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 33 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 33 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 33 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 33 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 7 trang 33 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 22 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 22 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 22 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 22 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 22 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 23 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 23 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 8 trang 23 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 9 trang 23 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 10 trang 23 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 11 trang 23 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 12 trang 23 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
-


Có bao nhiêu cặp số nguyên \(\left( x;y \right)\) thỏa mãn \(0\le x\le 4000\) và \(5\left( {{25}^{y}}+2y \right)=x+{{\log }_{5}}{{\left( x+1 \right)}^{5}}-4\)?
Theo dõi (0) 1 Trả lời




