Hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 8 Bài 5 Góc giữa đường thẳng và mặt phẳng. Góc nhị diện môn Toán học lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khởi động trang 82 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
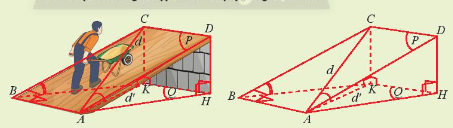
Mặt phẳng nghiêng thường được sử dụng trong lao động vì tính tiện dụng của nó. Quan sát hình mặt phẳng nghiêng (P) và mặt đất (Q) trong hình dưới đây và tìm hiểu tại sao:
\(\widehat{CAK}\) được gọi là góc hợp bởi đường thẳng d và (Q)
\(\widehat{CBK}\) được gọi là góc hợp bởi hai mặt phẳng (P) và (Q)
-
Hoạt động khám phá 1 trang 82 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\).
a) Trong trường hợp \(a\) vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và một đường thẳng \(b\) tuỳ ý trong \(\left( P \right)\).
b) Trong trường hợp \(a\) không vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và đường thẳng \(a'\) là hình chiếu vuông góc của \(a\) trên \(\left( P \right)\).
-
Thực hành 1 trang 83 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Cho hình lập phương \(ABCD.A'B'C'D'\). Tính góc giữa các đường thẳng sau đây với mặt phẳng \(\left( {ABCD} \right)\):
a) \(AA'\);
b) \(BC'\);
c) \(A'C\).
-
Vận dụng 1 trang 83 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
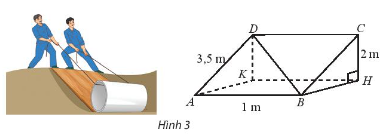
Một tấm ván hình chữ nhật \(ABCD\) được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết \(AB = 1\,m,AD = 3,5{\rm{ }}m\). Tính góc giữa đường thẳng \(BD\) và đáy hồ.
- VIDEOYOMEDIA
-
Hoạt động khám phá 2 trang 84 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
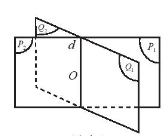
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\). Hãy gọi tên các nửa mặt phẳng có chung bờ \(d\). Các nửa mặt phẳng này chia không gian thành bao nhiêu phần?
-
Hoạt động khám phá 3 trang 84 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
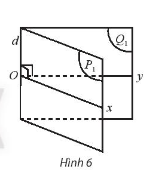
Cho góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\). Gọi \(O\) là một điểm tuỳ ý trên \(d\). \(Ox\) là tia nằm trong \(\left( P \right)\) và vuông góc với \(d\), \(Oy\) là tia nằm trong \(\left( Q \right)\) và vuông góc với \(d\) (Hình 6).
a) Nêu nhận xét về vị trí tương đối giữa \(d\) và \(mp\left( {Ox,Oy} \right)\).
b) Nêu nhận xét về số đo của góc \(xOy\) khi \(O\) thay đổi trên \(d\).
-
Thực hành 2 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Cho hình chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy và có tất cả các cạnh đều bằng \(a\). Xác định và tính góc phẳng nhị diện:
a) \(\left[ {S,BC,O} \right]\);
b) \(\left[ {C,SO,B} \right]\).
-
Vận dụng 2 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy.
(Nguồn: https://en.wikipedia.org/wiki/Memphis Pyramid)
-
Giải Bài 1 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
-
Giải Bài 2 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và có tất cả các cạnh bằng nhau.
a) Tìm góc giữa đường thẳng \(SA\) và \(\left( {ABCD} \right)\).
b) Tim góc phẳng nhị diện \(\left[ {A,SO,B} \right];\left[ {S,AB,O} \right]\).
-
Giải Bài 3 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Cho hình chóp cụt lục giác đều \(ABCDEF.A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\)
a) Tìm góc giữa cạnh bên và mặt đáy.
b) Tìm góc phẳng nhị diện \(\left[ {O,AB,A'} \right];\left[ {O',A'B',A} \right]\).
-
Giải Bài 4 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
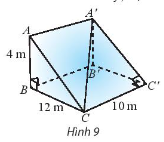
Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9.
a) Tính số đo góc giữa đường thẳng \(CA'\) và .
b) Tính số đo góc nhị diện cạnh \(CC'\).
-
Giải Bài 5 trang 85 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
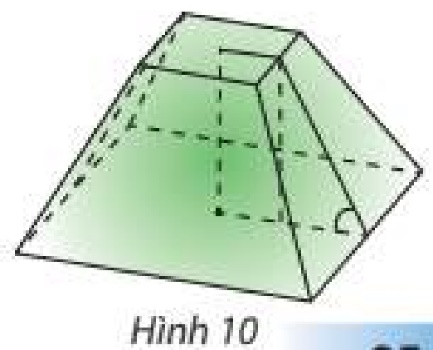
Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
-
Bài tập 1 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Cho hình chóp S.ABC có đáy là hình vuông tâm O cạnh a, SA = và vuông góc với đáy. Xác định và tính góc giữa:
a) SB và (ABCD);
b) SC và (ABCD);
c) SD và (ABCD);
d) SB và (SAC).
-
Bài tập 2 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 3. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm I của cạnh AB. Biết rằng mặt bên (SAB) là tam giác vuông cân tại S. Xác định và tính góc giữa:
a) SA và (ABC);
b) SC và (SAB).
-
Bài tập 3 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng . Tính số đo góc phẳng nhị diện [S, BC, A]?
-
Bài tập 4 trang 73 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Cho hình chóp S.ABC có SA ⊥ (ABC). Tam giác ABC vuông tại A, , AC = a, . Tính số đo góc phẳng nhị diện [S, BC, A]?


