Giải bài 3 tr 60 sách GK Toán Hình lớp 11
Cho tứ diện ABCD. Gọi M, N lần lượt là trung đểm của các cạnh AB, CD và G là trung điểm của đoạn MN
a) Tìm giao điểm A' của đường thẳng AG và mặt phẳng (BCD)
b) Qua M kẻ đường thẳng Mx song song với AA' và Mx cắt (BCD) tại M'. Chứng minh B, M', A' thẳng hàng và BM' = M'A' = A'N
c) Chứng minh GA = 3 GA'
Hướng dẫn giải chi tiết bài 3
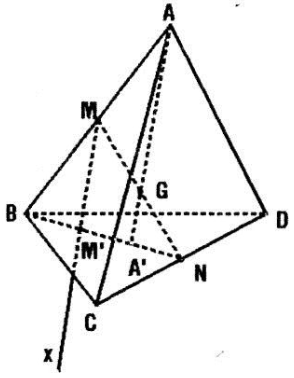
Câu a:
Ta có: \(G\in MN\Rightarrow G\in (ABN)\)
Gọi A' là giao điểm của AG và BN (trong mp (ABN))
Vì \((ABN)\cap (BCD)=AN\)
⇒ A' là giao điểm của AG và mp(BCD)
Câu b:
Ta có: Mx // AA'.
Mà M và AA' nằm trên mp(ABN)
⇒ Mx nằm trên mp(ABN)
Gọi M' là giao điểm của Mx và BN.
Vì \((ABN)\cap (BCD)=BN\Rightarrow M'\) là giao điểm của Mx và mp(BCD)
⇒ M', A', B nằm trên đường thẳng BN.
⇒ B, M', A' thẳng hàng.
Trong mp(ABN) xét \(\Delta NM'M\) có: G là trung điểm của MN, A'G // MM' ⇒ A'G là đường trung bình của \(\Delta NM'M\Rightarrow M'A'=A'N \ (2)\)
Từ (1) và (2) ⇒ BM' = M'A' = A'N.
Câu c:
Theo câu b) ta có:
NM' là đường trung bình của \(\Delta BAA'\Rightarrow AA'=2MM' \ (1)\)
A'G là trung bình của \(\Delta NM'M\Rightarrow MM'=2A'G \ (2)\)
Từ (1) và (2) \(\Rightarrow AA'=4GA'\)
\(\Rightarrow GA+GA'=4GA'\Rightarrow GA=3GA'\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 1 trang 59 SGK Hình học 11
Bài tập 2 trang 59 SGK Hình học 11
Bài tập 2.10 trang 67 SBT Hình học 11
Bài tập 2.11 trang 67 SBT Hình học 11
Bài tập 2.12 trang 67 SBT Hình học 11
Bài tập 2.13 trang 68 SBT Hình học 11
Bài tập 2.14 trang 68 SBT Hình học 11
Bài tập 2.15 trang 68 SBT Hình học 11
Bài tập 17 trang 55 SGK Hình học 11 NC
Bài tập 18 trang 55 SGK Hình học 11 NC
Bài tập 19 trang 55 SGK Hình học 11 NC
Bài tập 20 trang 55 SGK Hình học 11 NC
-


Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm khẳng định đúng.
bởi Đặng Ngọc Trâm
 22/01/2021
22/01/2021
A. giao tuyến của (SAB) và (IJG) là điểm G.
B. giao tuyến của (SAB) và (IJG) là SG.
C. giao tuyến của (SAB) và (IJG) là đường thẳng MG, với M là giao điểm của đường thẳng qua G và song song với AB với đường thẳng SA.
D. giao tuyến của (SAB) và (IJG) là đường thẳng MN, với N là giao điểm của IG với SB, M là giao điểm của JG với SA.
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Tìm thiết diện của (MAB) với hình chóp.
bởi Nguyễn Minh Hải
 22/01/2021
22/01/2021
A. thiết diện của (MAB) với hình chóp S.ABCD là tam giác MAB.
B. thiết diện của (MAB) với hình chóp, S.ABCD là tứ giác ABMN, với N là giao điểm của SD với đường thẳng đi qua M và song song với AB.
C. thiết diện của (MAB) với hình chóp S.ABCD là tứ giác ABMN, với N là giao điểm của MB và SD.
D. thiết diện của (MAB) với hình chóp S.ABCD là tứ giác ABMN, với N là giao điểm của MA và SD.
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Khẳng định nào sau đây là đúng?
bởi Kim Xuyen
 22/01/2021
22/01/2021
A. giao tuyến của (SAB) và (SCD) là điểm S.
B. giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và song song với AB.
C. giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và cắt AB.
D. giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và chéo nhau với AB.
Theo dõi (0) 1 Trả lời





