Giải bài 2.14 tr 68 SBT Hình học 11
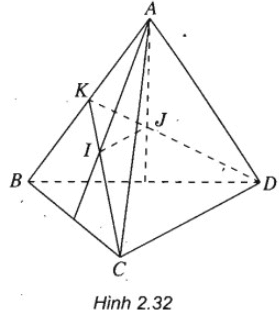
Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng: IJ // CD.
Hướng dẫn giải chi tiết
Gọi K là trung điểm của AB.
Vì I là trọng tâm của tam giác ABC nên I ∈ KC và vì J là trọng tâm của tam giác ABD nên J ∈ KD.
Từ đó suy ra \(\frac{{KI}}{{KC}} = \frac{{KJ}}{{KD}} = \frac{1}{3} \Rightarrow IJ\parallel CD\).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 2.12 trang 67 SBT Hình học 11
Bài tập 2.13 trang 68 SBT Hình học 11
Bài tập 2.15 trang 68 SBT Hình học 11
Bài tập 17 trang 55 SGK Hình học 11 NC
Bài tập 18 trang 55 SGK Hình học 11 NC
Bài tập 19 trang 55 SGK Hình học 11 NC
Bài tập 20 trang 55 SGK Hình học 11 NC
-


Chứng minh BC ⊥ SA?
bởi Truong Thi Hien
 28/06/2020
28/06/2020
Trả lời câu 7 vs
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Khẳng định nào sau đây sai?
bởi le thi my huyen
 18/06/2020
18/06/2020
Cho hình chop S.ABCD có đáy là hình chữ nhật tâm I, cạnh bên SA vuông góc với đấy. Khẳng định nào sau đây sai?
A. (SIC) vuông (SAD)
B. (SHC) vuông (SIA)
C. (SCD) vuông (SAI)
D. (SBD) vuông (SAC)
Theo dõi (1) 0 Trả lời -


Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, AB=a, AD=6a, SA vuông góc (ABCD), SA=2a. Tính góc giữa SB và (SAC), SA và (SBD)
bởi Nguyễn Trang
 23/03/2020
23/03/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời