Bài tập 14 trang 18 SGK Hình học 11 NC

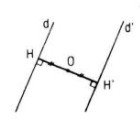
a) Kẻ OH ⊥ d(H ∈ d) thì vì d không đi qua O nên H không trùng với O

Phép đối xứng tâm Đ_O biến H thành H’ thì O là trung điểm của HH’, và biến đường thẳng  d thành đường thẳng d’ vuông góc với OH’ tại H’.

Suy ra d và d’ song song, cách đều điểm O

b) Nếu d không đi qua điểm O thì theo câu a), d’ // d nên d’ không trùng với d.

Nếu d đi qua O thì mọi điểm M ∈ d biến thành điểm M′ ∈ d′ .

-- Mod Toán 11 HỌC247