Học247 xin gửi đến các em tóm tắt Bài Giá trị lượng giác của góc lượng giác trong chương trình Toán 11 Chân trời sáng tạo. Bài giảng này nhằm giúp các em nắm vững kiến thức một cách nhanh chóng và hiệu quả, đồng thời cung cấp phương pháp giải bài tập và áp dụng vào các bài tập tương tự. Hy vọng các em sẽ học tập tốt và đạt được thành tích cao tại trường học.
Tóm tắt lý thuyết
1.1. Giá trị lượng giác của góc lượng giác
Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo a. Khi đó:
|
- Tung độ \(y_M\) của điểm M được gọi là sin của \(\alpha\), kí hiệu là sin\(\alpha\). - Hoành độ \(x_M\) của điểm M được gọi là côsin của \(\alpha\), kí hiệu là cos\(\alpha\). - Nếu \(x_M\) ≠ 0 thì tỉ số \({y_M \over x_M} ={\sin \alpha \over \cos \alpha}\) được gọi là tang của \(\alpha\), kí hiệu là tan\(\alpha\). - Nếu \(y_M\) ≠ 0 thì tỉ số \({x_M \over y_M} ={\cos \alpha \over \sin \alpha}\) được gọi là côtang của \(\alpha\), kí hiệu là cot\(\alpha\). - Các giá trị sin\(\alpha\), cos\(\alpha\), tan\(\alpha\), cot\(\alpha\) được gọi là các giá trị lượng giác của \(\alpha\). |
Chú ý:
+) Ta gọi trục hoành là trục cô sin, còn trục tung là trục sin.
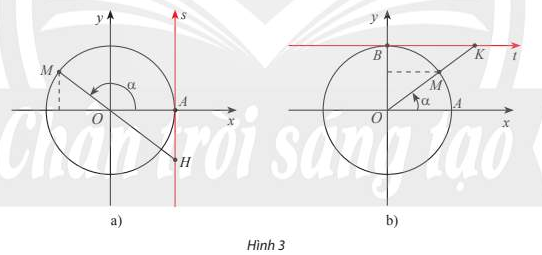
- Trục As có gốc ở điểm (1;0) và song song với trục sin (Hình 3a) gọi là trục tang. Nếu đường thẳng OM cắt trục tang thì tung độ của giao điểm đó chính là tan\(\alpha\).
- Trục Bt có gốc ở điểm B(0; 1) và song song với trục côsin (Hình 3b) gọi là trục cô tang. Nếu đường thẳng OM cắt trục côtang thì hoành độ của giao điểm đó chính là cot\(\alpha\).
+) sin\(\alpha\) và cos\(\alpha\) xác định với mọi \(\alpha \in \mathbb{R}\).
tan\(\alpha\) chỉ xác định khi \(\alpha\ne {\pi\over 2} + k\pi, (k\in \mathbb{Z})\).
cot\(\alpha\) chỉ xác định khi \(\alpha\ne {\pi} + k\pi, (k\in \mathbb{Z})\).
+) Với mọi góc lượng giác \(\alpha\) và số nguyên k, ta có
\(\sin (\alpha +k2\pi)=\sin \alpha\);
\(\cos (\alpha +k2\pi)=\cos \alpha\);
\(\tan (\alpha +k\pi)=\tan \alpha\);
\(\cot (\alpha +k\pi)=\cot \alpha\).
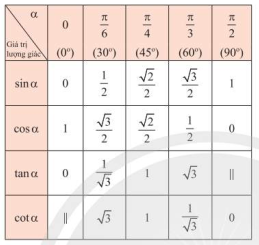
+) Giá trị lượng giác của một số góc \(\alpha\) đặc biệt với \(0\le \alpha \le {\pi \over 2}\) (hay \(0^0\le \alpha \le 90^0\)) như sau:
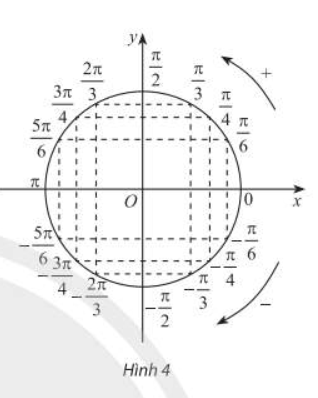
Sử dụng bảng trên và Hình 4, ta có thể xác định được giá trị lượng giác của một số góc đặc biệt khác.
1.2. Tính giá trị lượng giác của một góc bằng máy tính
Ta có thể tính giá trị lượng giác của một góc lượng giác bất kì bằng máy tính cầm tay. Lưu ý trước khi tính, cần chọn đơn vị đo góc như sau:
- Lần lượt ấn các phím 

- Tiếp tục ấn phím 

- Ấn các phím 
1.3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
Ta có các hệ thức sau liên hệ giữa các giá trị lượng giác của cùng một góc lượng giác.
|
\(\begin{array}{l} \bullet \,\,{\sin ^2}a + {\cos ^2}a = 1\\ \bullet \,\, 1 + {\tan ^2}a = \frac{1}{{{{\cos }^2}a}}\left( {a \ne \frac{\pi }{2} + k\pi ,k \in Z} \right)\\ \bullet \,\,1 + {\cot ^2}a = \frac{1}{{{{\sin }^2}a}}\left( {a \ne k\pi ,k \in Z} \right)\\ \bullet \,\, \tan a.\cot a = 1 \end{array}\) |
1.4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
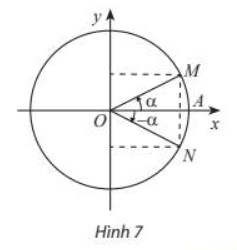
- Hai góc đối nhau: a và - a.
|
\(\cos \left( { - a} \right) = \cos a\\ \sin \left( { - a} \right) = - \sin a\\ \tan \left( { - a} \right) = - \tan a\\ \cot \left( { - a} \right) = - \cot a.\) |
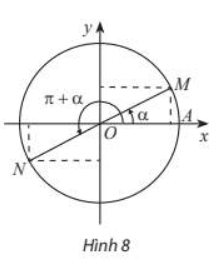
- Hai góc hơn kém nhau\(\pi\): a và \({\pi} { a} \).
|
\(\sin \left(\pi {+ a} \right) = - \sin a\\ \cos \left(\pi { + a} \right) = -\cos a\\ \tan \left(\pi {+a} \right) = \tan a\\ \cot \left(\pi {+ a} \right) = \cot a.\) |
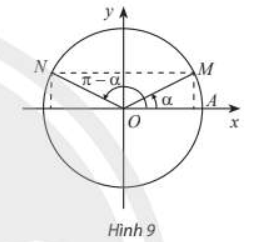
- Hai góc bù nhau: a và \(\pi { - a}\).
|
\(\sin \left(\pi { - a} \right) = \sin a\\ \cos \left(\pi { - a} \right) = -\cos a\\ \tan \left(\pi { - a} \right) = - \tan a\\ \cot \left(\pi { - a} \right) = - \cot a.\) |
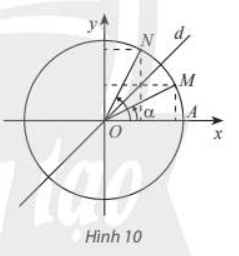
- Góc phụ nhau: a và \({\pi \over 2} { - a} \).
|
\(\sin \left({\pi \over 2} { - a} \right) = \cos a\\ \cos \left({\pi \over 2} { - a} \right) = \sin a\\ \tan \left({\pi \over 2} { - a} \right) = \cot a\\ \cot \left({\pi \over 2} { - a} \right) = \tan a.\) |
Bài tập minh họa
Câu 1: Giá trị của biểu thức
a) \(P=\sin x\) với \(x=420{}^\circ \).
b) \(\cot \frac{81\pi }{4}\)
Hướng dẫn giải
a) Ta có \(420{}^\circ =\frac{7\pi }{3}=\frac{\pi }{3}+2\pi \)
\(P=\sin 420{}^\circ =\sin \left( \frac{\pi }{3}+2\pi \right)=\sin \frac{\pi }{3}=\frac{\sqrt{3}}{2}\)
b) Ta có: \(\cot \frac{81\pi }{4}=\cot \left( \frac{\pi }{4}+20\pi \right)=\cot \frac{\pi }{4}=1\).
Câu 2: Cho \(\tan \alpha =-2\). Khi đó giá trị \(\sin \alpha .\cos \alpha \) gần nhất với giá trị nào sau đây?
A. \(-2\) B. \(-1\) C. 1 D. 2
Hướng dẫn giải
\(\tan \alpha =-2\Rightarrow \frac{1}{{{\cos }^{2}}\alpha }=1+{{\tan }^{2}}\alpha =1+4=5\)
\(\Rightarrow {{\cos }^{2}}\alpha =\frac{1}{5}\Rightarrow {{\sin }^{2}}\alpha =1-{{\cos }^{2}}\alpha =1-\frac{4}{5}=\frac{4}{5}\)
Mặt khác ta thấy \(\tan \alpha =-2=\frac{\sin \alpha }{\cos \alpha }\) nên \(\sin \alpha ,\cos \alpha \) trái dấu
\(\Rightarrow \sin \alpha .\cos \alpha =-\sqrt{\frac{4}{25}}=\frac{-2}{5}\).
Luyện tập Bài 2 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Biết và tính được các giá trị lượng giác của các góc lượng giác.
- Sử dụng được các hệ thức cơ bản giữa các giá trị lượng giác và giải quyết được một số vấn đề thực tiễn gắn với giá trị lượng giác của góc lượng giác.
3.1. Trắc nghiệm Bài 2 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 1 Bài 2 cực hay có đáp án và lời giải chi tiết.
-
- A. \(\frac{\sqrt{3}}{2}\)
- B. \(-\frac{\sqrt{3}}{2}\)
- C. \(\frac{1}{2}\)
- D. \(-\frac{1}{2}\)
-
- A. \(\frac{\sqrt{2}}{2}\)
- B. \(-1\)
- C. \(-\frac{\sqrt{2}}{2}\)
- D. 1
-
- A. \(\frac{3}{5}\)
- B. \(\frac{-3}{5}\)
- C. \(\pm \frac{3}{5}\)
- D. \(\frac{9}{25}\)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 2 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 1 Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 15 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 16 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 16 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 17 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 17 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 19 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 7 trang 20 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 8 trang 20 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 51 trang 14 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 11 trang 15 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Hỏi đáp Bài 2 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247