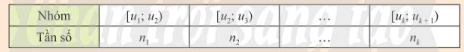Chúng ta hôm nay sẽ đến với một bài học thú vị về thống kê trong môn Toán lớp 11 Chân trời sáng tạo, và chủ đề chính là "Số trung bình và mốt của mẫu số liệu ghép nhóm". Đặt chân vào thế giới số liệu, chúng ta sẽ khám phá cách áp dụng các khái niệm khoa học này để hiểu và phân tích dữ liệu một cách chính xác.
Tóm tắt lý thuyết
1.1. Số liệu ghép nhóm
Mẫu số liệu ghép nhóm thường được trình bày dưới dạng bảng thống kê có dạng như sau:
Bảng 1: Bảng tần số ghép nhóm
Chú ý:
+ Bảng trên gồm 4 nhóm [uj ; uj + 1) với 1 \(\le\)j\(\le\)k, mỗi nhóm gồm một số giá trị được ghép theo một tiêu chí xác định.
+ Cỡ mẫu \(n = {m_1} + {m_2} + ... + {m_k}\).
+ Giá trị chính giữa mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm [u1 ; u2) có giá trị đại diện là \(\frac{{{u_1} + {u_{2}}}}{2}\).
+ Hiệu uj + 1 - uj được gọi là độ dài của nhóm [uj ; uj + 1).
Một số quy tắc ghép nhóm của mẫu số liệu
Mỗi mẫu số liệu có thể được ghép nhóm theo nhiều cách khác nhau nhưng thường tuân theo một số quy tắc sau.
- Sử dụng từ k = 5 đến k = 20 nhóm. Cỡ mẫu càng lớn thì cẩn càng nhiều nhóm số liệu. Các nhóm có cùng độ dài bằng L thoả mãn R < k . L, trong đó R là khoảng biến thiên, k là số nhóm.
- Giá trị nhỏ nhất của mẫu thuộc vào nhóm [u1 ; u2) và càng gần u1 càng tốt. Giá trị lớn nhất của mẫu thuộc nhóm [uk ; uk + 1) và càng gần uk + 1 càng tốt.
1.2. Số trung bình
Giả sử mẫu số liệu được cho dưới dạng băng tần số ghép nhóm
Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\overline{x}\) và được tính bởi công thức sau:
|
\[\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\] |
trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
Ý nghĩa của số trung bình của mẫu số liệu ghép nhóm
Số trung bình của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho số trung bình của mẫu số liệu gốc. Nó thường dùng để đo xu thế trung tâm của mẫu số liệu.
1.3. Mốt
Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Giả sử nhóm chứa mốt là [um ; um + 1), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là Mo, được xác định bởi công thức
|
\({M_o} = {a_j} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.(u_{m + 1}-u_{m}).\) |
Chú ý: Nếu không có nhóm kề trước của nhóm chứa mốt thì \(n_{m - 1}\) = 0. Nếu không có nhóm kể sau của nhóm chứa mốt thì \(n_{m + 1}\) = 0.
Ý nghĩa của mốt của mẫu số liệu ghép nhóm
– Mốt của mẫu số liệu không ghép nhóm là giá trị có khả năng xuất hiện cao nhất khi lấy mẫu Mốt của mẫu số liệu sau khi ghép nhóm Mo, xấp xỉ với mốt của mẫu số liệu không ghép nhóm. Các giá trị nằm xung quanh Mo thường có khả năng xuất hiện cao hơn các giá trị khác.
– Một mẫu số liệu ghép nhóm có thể có nhiều nhóm chứa mốt và nhiều mốt.
Bài tập minh họa
Câu 1: Theo dõi thời gian đi từ nhà đến trường của bạn A trong 35 ngày, ta có bảng số liệu sau: (đơn vị phút)
Tính số trung bình của mẫu (chính xác đến hàng phần trăm).
Hướng dẫn giải
\(\overline{x}\)\( =\frac{5\times 20+9\times 22+10\times 24+7\times 26+4\times 28}{35}\)\( =\frac{832}{35}\approx 23,77\)(phút)
Luyện tập Bài 1 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Tính được các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm: số trung bình cộng (hay số trung bình), mốt.
- Hiểu được ý nghĩa và vai trò của các số đặc trưng nói trên của mẫu số liệu trong thực tiễn.
3.1. Trắc nghiệm Bài 1 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 5 Bài 1 cực hay có đáp án và lời giải chi tiết.
-
- A. bảng tần suất
- B. bảng tần số
- C. thứ tự tăng dần
- D. thứ tự giảm dần
-
- A. 4.36
- B. 10.3695
- C. 8.4375
- D. 9.325
-
- A. các giá trị của số liệu được ghép nhóm theo nhiều tiêu chí xác định.
- B. các giá trị của số liệu được ghép nhóm theo hai tiêu chí xác định.
- C. các giá trị của số liệu được ghép nhóm theo một tiêu chí xác định.
- D. các giá trị của số liệu được ghép nhóm theo ba tiêu chí xác định.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 1 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 5 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 130 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 130 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 132 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 132 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 133 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 133 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 133 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 134 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 134 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 135 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 135 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 135 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 149 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 149 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 149 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 150 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 150 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 150 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Hỏi đáp Bài 1 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247