Giải bài 8 trang 104 SGK Toán 10 Cánh diều tập 2
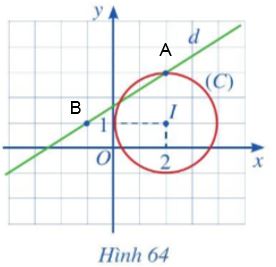
Quan sát Hình 64 và thực hiện các hoạt động sau:
a. Lập phương trình đường thẳng d
b. Lập phương trình đường tròn (C)
c. Lập phương trình tiếp tuyến của đường tròn (C) tại điểm \(M(2+\sqrt{2};1+\sqrt{2})\)
Hướng dẫn giải chi tiết Bài 8
Phương pháp giải
+ Phương trình tham số của đường thẳng là:
\(\left\{ \begin{array}{l}
x = {x_0} + at\\
y = {y_0} + bt
\end{array} \right.\;\;\;\;\;\;\;\;\)
+ Phương trình tổng quát dạng ax + by + c =0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.
+ Điểm \(M\left( {x;y} \right)\) thuộc đường tròn (C), tâm ((a; b), bán kính R khi và chỉ khi
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\). (1)
Ta gọi (1) là phương trình của đường tròn (C).
+ Phương trình tiếp tuyến của đường tròn tâm I(a, b) tại điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn là:
\(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\)
Hướng dẫn giải
a. (d) qua B(-1;1) và A(2; 3) => (d) nhận \(\overrightarrow{BA}=(3;2)\) làm vecto chỉ phương.
\(\Rightarrow\) (d): \(\left\{ \begin{align} x=-1+3t \\ y=1+2t \\\end{align} \right.\) (t là tham số)
b. (C) có tâm I(2; 1), có bán kính R = \(AI=\sqrt{{{(2-2)}^{2}}+{{(1-3)}^{2}}}=2\)
\(\Rightarrow\) (C) có phương trình: \({{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4\)
c. Lập phương trình tiếp tuyến của đường tròn (C) tại điểm \(M(2+\sqrt{2};1+\sqrt{2})\)
Phương trình tiếp tuyến \(\Delta \) của đường tròn (C) tại điểm \(M(2+\sqrt{2};1+\sqrt{2})\), có vecto pháp tuyến \(\overrightarrow{IM}=(\sqrt{2};\sqrt{2})\) là:
\(\sqrt{2}(x-2-\sqrt{2})+\sqrt{2}(y-1-\sqrt{2})=0\)
hay (\(\Delta \)): \(\sqrt{2}x+\sqrt{2}y-3\sqrt{2}-4=0\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 6 trang 103 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 7 trang 103 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 9 trang 104 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 10 trang 104 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 11 trang 104 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 71 trang 97 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 72 trang 97 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 73 trang 98 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 74 trang 98 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 75 trang 98 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 76 trang 98 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 77 trang 98 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 78 trang 98 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 79 trang 98 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 80 trang 99 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 81 trang 99 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 82 trang 99 SBT Toán 10 Cánh diều tập 2 - CD
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.