Giải bài 6 trang 79 SBT Toán 10 Chân trời sáng tạo tập 1
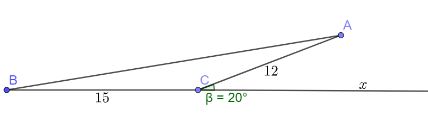
Một chiếc tàu khởi hành từ bến cảng, đi về hướng Bắc 15km, sau đó bẻ lái \(20^\circ \) về hướng Tây Bắc và đi thêm 12 km nữa (hình 9). Tính khoảng cách từ tàu đến bến cảng.
Hướng dẫn giải chi tiết Bài 6
Phương pháp giải
Áp dụng định lí côsin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Lời giải chi tiết
Góc \(\widehat {ACx}\) là góc bù với góc \(\widehat {ACB}\), suy ra \(\widehat {ACB} = 180^\circ - \widehat {ACx} = 180^\circ - 20^\circ = 160^\circ \)
Áp dụng định lí côsin vào tam giác ABC ta có:
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2AC.BC.\cos C\\ \Rightarrow AB = \sqrt {A{C^2} + B{C^2} - 2AC.BC.\cos C} = \sqrt {{{12}^2} + {{15}^2} - 2.12.15.\cos 160^\circ } \simeq 26,6\end{array}\)
Vậy khoảng cách từ tàu đến bến cảng xấp xỉ 26,6 km
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.