HÆ°áŧng dášŦn GiášĢi bà i tášp ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo ChÆ°ÆĄng 8 Bà i 1 Quy tášŊc cáŧng và quy tášŊc nhÃĒn giÚp cÃĄc em háŧc sinh nášŊm váŧŊng phÆ°ÆĄng phÃĄp giášĢi bà i tášp và Ãīn luyáŧn táŧt kiášŋn tháŧĐc.
-
Hoᚥt Äáŧng khÃĄm phÃĄ 1 trang 20 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Trong máŧt cáŧ§a hà ng bÃĄn kem cÃģ 5 loᚥi kem que và 4 loᚥi kem áŧc quášŋ nhÆ° hÃŽnh 1. CÃģ bao nhiÊu cÃĄch cháŧn mua máŧt loᚥi kem que hoáš·c máŧt kem áŧc quášŋ áŧ cáŧ§a hà ng nà y?
-
Tháŧąc hà nh 1 trang 21 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Hà cÃģ 5 cuáŧn sÃĄch khoa háŧc, 4 cuáŧn sÃĄch tiáŧu thuyášŋt và 3 cuáŧn truyáŧn tranh (cÃĄc sÃĄch khÃĄc nhau táŧŦng ÄÃīi máŧt). Hà Äáŧng Ã― cho Nam mÆ°áŧĢn máŧt cuáŧn sÃĄch trong sáŧ ÄÃģ Äáŧ Äáŧc. Nam cÃģ bao nhiÊu cÃĄch cháŧn máŧt cuáŧn sÃĄch Äáŧ mÆ°áŧĢn?
-
Hoᚥt Äáŧng khÃĄm phÃĄ 2 trang 21 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
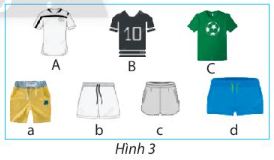
An cÃģ 3 chiášŋc ÃĄo và 4 chiášŋc quᚧn tháŧ thao. An muáŧn cháŧn máŧt báŧ quᚧn ÃĄo trong sáŧ ÄÃģ Äáŧ máš·c chÆĄi tháŧ thao cuáŧi tuᚧn nà y.
a) Váš― và o váŧ và hoà n thà nh sÆĄ Äáŧ hÃŽnh cÃĒy nhÆ° hÃŽnh 4 Äáŧ tháŧ hiáŧn tášĨt cášĢ cÃĄc khášĢ nÄng mà An cÃģ tháŧ láŧąa cháŧn máŧt báŧ quᚧn ÃĄo.
b) An cÃģ bao nhiÊu cÃĄch láŧąa cháŧn báŧ quᚧn ÃĄo? HÃĢy giášĢi thÃch.
-
Tháŧąc hà nh 2 trang 24 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Máŧt mášŦu xe Ãī tÃī cÃģ báŧn mà u ngoᚥi thášĨt là trášŊng, Äen, cam và bᚥc. MášŦu xe nà y cÅĐng cÃģ hai mà u náŧi thášĨt là Äen và xÃĄm.
a) KhÃĄch hà ng cÃģ bao nhiÊu láŧąa cháŧn váŧ mà u ngoᚥi thášĨt và náŧi thášĨt khi mua máŧt chiášŋc xe Ãī tÃī mášŦu nà y?
b) HÃĢy váš― sÆĄ Äáŧ hÃŽnh cÃĒy Äáŧ giášĢi thÃch cho kášŋt quášĢ tÃnh toÃĄn áŧ trÊn.
- VIDEOYOMEDIA
-
Tháŧąc hà nh 3 trang 24 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
CÃģ nhiáŧu nhášĨt bao nhiÊu Äoᚥn phÃĒn táŧ RNA khÃĄc nhau cháŧĐa 4 phÃĒn táŧ nucleotide, trong ÄÃģ:
a) KhÃīng cÃģ nucleotide A nà o?
b) CÃģ nucleotide A nášąm áŧ váŧ trà Äᚧu tiÊn?
-
Vášn dáŧĨng trang 24 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Trong phᚧn kháŧi Äáŧng Äᚧu bà i háŧc nà y, nášŋu cÃīng ty cÃģ 2500 nhÃĒn viÊn thÃŽ sáŧ mÃĢ sáŧ nhÆ° vášy cÃģ Äáŧ§ Äáŧ cášĨp cho máŧi nhÃĒn viÊn máŧt mÃĢ sáŧ riÊng hay khÃīng?
-
GiášĢi bà i 1 trang 24 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Máŧt thÃđng cháŧĐa 6 quášĢ dÆ°a hášĨu, máŧt thÃđng khÃĄc cháŧĐa 15 quášĢ thanh long. TáŧŦ hai thÃđng nà y,
a) cÃģ bao nhiÊu cÃĄch cháŧn máŧt quášĢ dÆ°a hášĨu hoáš·c máŧt quášĢ thanh long.
b) cÃģ bao nhiÊu cÃĄch cháŧn máŧt quášĢ dÆ°a hášĨu và 1 quášĢ thanh long.
-
GiášĢi bà i 2 trang 24 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Tung Äáŧng tháŧi máŧt Äáŧng xu và máŧt con sÚc sášŊc, nhášn ÄÆ°áŧĢc kášŋt quášĢ là máš·t xuášĨt hiáŧn trÊn Äáŧng xu (sášĨp hay ngáŧa) và sáŧ chášĨm xuášĨt hiáŧn trÊn con xÚc xášŊc.
a) TÃnh sáŧ kášŋt quášĢ cÃģ tháŧ xášĢy ra
b) Váš― sÆĄ Äáŧ hÃŽnh cÃĒy và liáŧt kÊ tášĨt cášĢ cášĢ cÃĄc kášŋt quášĢ ÄÃģ.
-
GiášĢi bà i 3 trang 25 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Tᚥi máŧt nhà hà ng chuyÊn pháŧĨc váŧĨ cÆĄm trÆ°a vÄn phÃēng, tháŧąc ÄÆĄn cÃģ 5 mÃģn chÃnh, 3 mÃģn pháŧĨ và 4 loᚥi Äáŧ uáŧng. Tᚥi ÄÃĒy tháŧąc khÃĄch cÃģ bao nhiÊu cÃĄch cháŧn báŧŊa trÆ°a gáŧm máŧt mÃģn chÃnh, máŧt mÃģn pháŧĨ và máŧt loᚥi Äáŧ uáŧng.
-
GiášĢi bà i 4 trang 25 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
CÃģ bao nhiÊu sáŧ táŧą nhiÊn cÃģ 3 cháŧŊ sáŧ, trong ÄÃģ cháŧŊ sáŧ hà ng trÄm là cháŧŊ sáŧ chášĩn, cháŧŊ sáŧ hà ng ÄÆĄn váŧ là cháŧŊ sáŧ lášŧ.
-
GiášĢi bà i 5 trang 25 SGK ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
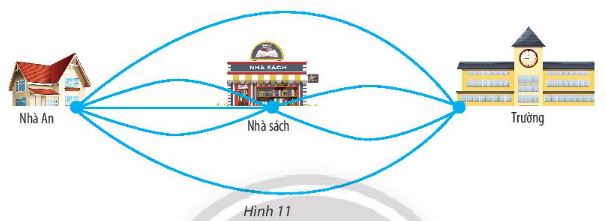
An cÃģ tháŧ Äi táŧŦ nhà Äášŋn trÆ°áŧng theo cÃĄc con ÄÆ°áŧng nhÆ° hÃŽnh 11, trong ÄÃģ cÃģ nháŧŊng con ÄÆ°áŧng Äi qua nhà sÃĄch.
a) An cÃģ bao nhiÊu cÃĄch Äi táŧŦ nhà Äášŋn trÆ°áŧng mà cÃģ Äi qua nhà sÃĄch?
b) An cÃģ bao nhiÊu cÃĄch Äi táŧŦ nhà Äášŋn trÆ°áŧng?
LÆ°u Ã―: Cháŧ tÃnh nháŧŊng ÄÆ°áŧng Äi qua cÃĄc Äiáŧm (nhà An, nhà sÃĄch, nhà trÆ°áŧng) khÃīng quÃĄ 1 lᚧn
-
GiášĢi bà i 1 trang 39 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Trong máŧt cÃĄi háŧp cÃģ cháŧĐa 8 quášĢ bÃģng mà u trášŊng ÄÃĄnh sáŧ táŧŦ 1 Äášŋn 8; 10 quášĢ mà u xanh ÄÃĄnh sáŧ táŧŦ 1 Äášŋn 10; 12 quášĢ bÃģng mà u cam ÄÃĄnh sáŧ táŧŦ 1 Äášŋn 12. TáŧŦ háŧp nà y, cÃģ bao nhiÊu cÃĄch?
a) cháŧn ra máŧt quášĢ bÃģng?
b) cháŧn ra ba quášĢ bÃģng cÃģ mà u khÃĄc nhau ÄÃīi máŧt?
c) cháŧn ra hai quášĢ bÃģng cÃģ mà u khÃĄc nhau?
-
GiášĢi bà i 2 trang 39 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
CÃģ ba cÃĄi háŧp, háŧp tháŧĐ nhášĨt cháŧĐa 2 quášĢ cᚧu dÃĄn nhÃĢn A, B; Háŧp tháŧĐ hai cháŧĐa 3 quášĢ cᚧu dÃĄn nhÃĢn a, b, c. Háŧp tháŧĐ ba cÃģ 2 quášĢ cᚧu dÃĄn nhÃĢn 1, 2. TáŧŦ máŧi háŧp lášĨy ra ngášŦu nhiÊn máŧt quášĢ cᚧu.
a) HÃĢy váš― sÆĄ Äáŧ cÃĒy Äáŧ tháŧ hiáŧn tášĨt cášĢ cÃĄc kášŋt quášĢ cÃģ tháŧ xášĢy ra.
b) CÃģ bao nhiÊu kášŋt quášĢ cÃģ tháŧ xášĢy ra?
-
GiášĢi bà i 3 trang 39 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Ba láŧp cáŧ§a máŧt trÆ°áŧng Äang lÊn kášŋ hoᚥch Äáŧ Äi dÃĢ ngoᚥi, máŧt láŧp cÃģ tháŧ cháŧn máŧt trong nÄm Äáŧa Äiáŧm. CÃģ bao nhiÊu kášŋt quášĢ cÃģ tháŧ xášĢy ra váŧ cÃĄch cháŧn Äáŧa Äiáŧm cáŧ§a ba láŧp?
-
GiášĢi bà i 4 trang 39 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
MÃĢ xÃĄc tháŧąc (OTP â One Time Password) do máŧt ngÃĒn hà ng gáŧi và o Äiáŧn thoᚥi cáŧ§a khÃĄch hà ng cho máŧi lᚧn giao dáŧch là máŧt dÃĢy sáŧ 6 kà táŧą táŧŦ cÃĄc cháŧŊ sáŧ táŧŦ 0 Äášŋn 9. CÃģ tháŧ tᚥo ra bao nhiÊu mÃĢ xÃĄc tháŧąc khÃĄc nhau nhÆ° vášy?
-
GiášĢi bà i 5 trang 39 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Tung máŧt Äáŧng xu 5 lᚧn liÊn tiášŋp và ghi lᚥi kášŋt quášĢ (và dáŧĨ dÃđng kà hiáŧu SSNSN Äáŧ cháŧ kášŋt quášĢ 5 lᚧn tung lᚧn lÆ°áŧĢt là sášĨp, sášĨp, ngáŧa, sášĨp, ngáŧa). CÃģ bao nhiÊu kášŋt quášĢ khÃĄc nhau cÃģ tháŧ xášĢy ra?
-
GiášĢi bà i 6 trang 40 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
MÃĢ sáŧ máŧt nhÃĒn viÊn cáŧ§a máŧt cÃīng ty cÃģ 4 kà táŧą, gáŧm máŧt cháŧŊ cÃĄi Äᚧu tÊn (táŧŦ 6 cháŧŊ cÃĄi A, B, C, D, E, F) và tiášŋp theo là 3 cháŧŊ sáŧ (táŧŦ cÃĄc cháŧŊ sáŧ 0; 1; 2; 3; 4; 5; 6; 7; 8; 9). CÃīng ty cÃģ tháŧ tᚥo ra bao nhiÊu mÃĢ sáŧ nhÃĒn viÊn theo cÃĄch nà y?
-
GiášĢi bà i 7 trang 40 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
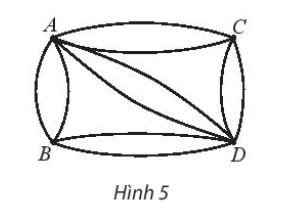
CÃģ cÃĄc con ÄÆ°áŧng náŧi báŧn ngÃīi là ng A, B, C, D nhÆ° trong HÃŽnh 5. CÃģ bao nhiÊu cÃĄch cháŧn ÄÆ°áŧng Äi khÃĄc nhau
a) táŧŦ A qua B ráŧi Äášŋn D
b) táŧŦ A Äášŋn D
LÆ°u Ã―: Máŧi ÄÆ°áŧng Äi qua máŧi ngÃīi là ng Ãt nhášĨt 1 lᚧn
-
GiášĢi bà i 8 trang 40 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Tung Äáŧng tháŧi hai con xÚc xášŊc khÃĄc nhau và ghi lᚥi sáŧ chášĨm xuášĨt hiáŧn trÊn máŧi con xÚc xášŊc. CÃģ bao nhiÊu kášŋt quášĢ cÃģ tháŧ xášĢy ra mà táŧng sáŧ chášĨm xuášĨt hiáŧn trÊn hai máš·t là báŧi cáŧ§a 5?
-
GiášĢi bà i 9 trang 40 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Sáŧ dáŧĨng 5 cháŧŊ sáŧ 0; 1; 2; 3; 4 cÃģ tháŧ lášp ÄÆ°áŧĢc bao nhiÊu sáŧ táŧą nhiÊn
a) cÃģ ba cháŧŊ sáŧ khÃĄc nhau?
b) cÃģ 3 cháŧŊ sáŧ khÃĄc nhau và bÃĐ hÆĄn 300?
c) cÃģ cÃĄc cháŧŊ sáŧ khÃĄc nhau và bÃĐ hÆĄn 100?
-
GiášĢi bà i 10 trang 40 SBT ToÃĄn 10 ChÃĒn tráŧi sÃĄng tᚥo tášp 2 - CTST
Máŧt khÃģa táŧ háŧĢp váŧi ÄÄĐa quay cÃģ 40 vᚥch sáŧ (xem hÃŽnh 7). Mášt mÃĢ cáŧ§a khÃģa là máŧt dÃĢy sáŧ gáŧm 3 sáŧ, kÃ― hiáŧu là a â b â c, máŧi sáŧ là máŧt sáŧ táŧą nhiÊn táŧŦ 0 Äášŋn 39. Äáŧ máŧ khÃģa, cᚧn quay máš·t sáŧ ngÆ°áŧĢc chiáŧu kim Äáŧng háŧ cho Äášŋn khi Äiáŧm máŧc gáš·p vᚥch sáŧ a lᚧn tháŧĐ ba, ráŧi quay máš·t sáŧ theo chiáŧu ngÆ°áŧĢc lᚥi cho Äášŋn khi Äiáŧm máŧc gáš·p vᚥch sáŧ b lᚧn tháŧĐ 2, cuáŧi cÃđng quay máš·t sáŧ ngÆ°áŧĢc chiáŧu kim Äáŧng háŧ cho Äášŋn khi Äiáŧm máŧc gáš·p vᚥch sáŧ c ÄÃĒu tiÊn. Nášŋu a, b, c phášĢi khÃĄc nhau ÄÃīi máŧt, thÃŽ cÃģ bao nhiÊu cÃĄch cháŧn cho khÃģa táŧ háŧĢp trÊn?