Giải bài 5 trang 25 SGK Toán 10 Chân trời sáng tạo tập 2
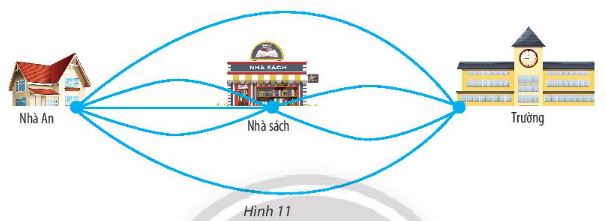
An có thể đi từ nhà đến trường theo các con đường như hình 11, trong đó có những con đường đi qua nhà sách.
a) An có bao nhiêu cách đi từ nhà đến trường mà có đi qua nhà sách?
b) An có bao nhiêu cách đi từ nhà đến trường?
Lưu ý: Chỉ tính những đường đi qua các điểm (nhà An, nhà sách, nhà trường) không quá 1 lần
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
a) Bước 1: Xác định số cách đi từ nhà đến nhà sách, từ nhà sách đến trường
Bước 2: Áp dụng quy tắc nhân
b) Bước 1: Xác định số cách đi từ nhà đến trường qua nhà sách
Bước 2: Xác định số cách đi từ nhà đến trường không qua nhà sách
Bước 3: Áp dụng quy tắc cộng
Lời giải chi tiết
a) Việc đi từ nhà đến trường qua nhà sách được thực hiện qua hai công đoạn:
Công đoạn 1: Đi từ nhà đến nhà sách, có 3 con đường
Công đoạn 2: Đi từ nhà sách đến trường, có 2 con đường
Số cách đi từ nhà đến trường qua nhà sách có số cách là:
\(3.2 = 6\)(cách)
b) Việc đi từ nhà đến trường có 2 phương án
Phương án 1: Đi từ nhà đến trường qua nhà sách, có 6 cách thực hiện (kết quả của câu a))
Phương án 2: Đi từ nhà đến trường không qua nhà sách có 2 cách
Áp dụng quy tắc cộng, ta có số cách đi từ nhà đến trường là:
\(6 + 2 = 8\) (cách)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 3 trang 25 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 25 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 39 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 39 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 39 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 39 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 39 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 40 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 7 trang 40 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 8 trang 40 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 9 trang 40 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 10 trang 40 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
-


Trong \(100000\) số nguyên dương đầu tiên, cho biết có bao nhiêu số chứa một chữ số \(3\), một chữ số \(4\) và một chữ số \(5\)?
bởi Khánh An
 12/09/2022
Theo dõi (0) 1 Trả lời
12/09/2022
Theo dõi (0) 1 Trả lời