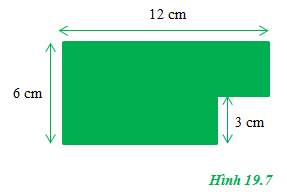
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật dài 12cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình 19.7)
Câu trả lời (1)
-
Hình vẽ biểu diễn lực:

Chia bản mỏng thành hai phần: ABCD và BMNQ. Trọng tâm của 2 phần này là O1 và O2. Nếu gọi trọng tâm của bản là G thì G sẽ là điểm đặt của hợp lực của các trọng lực P1 và P2 của hai bản nói trên.
Do các bản phẳng mỏng, đồng chất nên trọng lượng của mỗi tấm tỉ lệ với diện tích.
Ta có: \(\frac{{{P_1}}}{{{P_2}}} = \frac{{{S_1}}}{{{S_2}}} = \frac{{6.9}}{{3.3}} = 6\)
Khi đó G được xác định như sau:
\(\frac{{{P_1}}}{{{P_2}}} = \frac{{HI}}{{H{O_1}}} = \frac{{G{O_2}}}{{G{O_1}}} = 6 \Rightarrow G{O_2} = 6.G{O_1}\) (1)
Mặt khác ta có:
\(\begin{array}{*{20}{c}}
{}&{G{O_1} + G{O_2} = {O_1}{O_2} = \sqrt {{O_1}{I^2} + {O_2}{I^2}} }\\
{}&{ = \sqrt {{{\left( {4,5 + 1,5} \right)}^2} + {{1,5}^2}} = 6,18}\\
{}&{ \Rightarrow G{O_1} + G{O_2} = 6,18cm\left( 2 \right)}
\end{array}\)Từ (1) và (2) => GO1 = 0,88 cm
Vậy trọng tâm G nằm trên đường nối O1 và O2 và cách G1 một đoạn 0,88cm.
bởi Van Dung 22/01/2021
Like (0) Báo cáo sai phạm
22/01/2021
Like (0) Báo cáo sai phạm
Nếu bạn hỏi, bạn chỉ thu về một câu trả lời.
Nhưng khi bạn suy nghĩ trả lời, bạn sẽ thu về gấp bội!

Lưu ý: Các trường hợp cố tình spam câu trả lời hoặc bị báo xấu trên 5 lần sẽ bị khóa tài khoản
Các câu hỏi mới
-
A. \(v = \frac{{{d_1} + {d_2}}}{{{t_1} + {t_2}}}\)
B. \(v = \frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\)
C. \(v = \frac{{{d_1} + {d_2}}}{{{t_2} - {t_1}}}\)
D. \(v = \frac{{{d_2} - {d_1}}}{{{t_1} - {t_2}}}\)
24/11/2022 | 1 Trả lời
-
.png)
A. từ 0 đến \({t_2}\).
B. từ \({t_1}\) đến \({t_2}\) .
C. từ 0 đến \({t_1}\) và từ \({t_2}\) đến \({t_3}\).
D. từ 0 đến \({t_3}\).
23/11/2022 | 1 Trả lời
-
23/11/2022 | 1 Trả lời
-
VIDEOYOMEDIA
.png)
a) Hãy mô tả chuyển động.
b) Xác định tốc độ và vận tốc của chuyển động trong các khoảng thời gian:
- Từ 0 đến 0,5 giờ.
- Từ 0,5 đến 2,5 giờ.
- Từ 0 đến 3,25 giờ.
- Từ 0 đến 5,5 giờ.
24/11/2022 | 1 Trả lời
-
a) Tính vận tốc của hai người.
b) Viết phương trình chuyển động của hai người.
24/11/2022 | 1 Trả lời
-
.png)
23/11/2022 | 1 Trả lời
-
A. Chuyển động có độ dịch chuyển tăng đều theo thời gian.
B. Chuyển động có độ dịch chuyển giảm đều theo thời gian.
C. Chuyển động có độ dịch chuyển không đổi theo thời gian.
D. Chuyển động tròn đều.
24/11/2022 | 1 Trả lời
-
24/11/2022 | 1 Trả lời
-
23/11/2022 | 1 Trả lời
-
a) Tính sự thay đổi tốc độ của quả bóng.
b) Tính sự thay đổi vận tốc của quả bóng.
c) Tính gia tốc của quả bóng trong thời gian tiếp xúc với tường.
24/11/2022 | 1 Trả lời
-
.png)
a) Mô tả chuyển động của thang máy.
b) Tính gia tốc của thang máy trong các giai đoạn.
23/11/2022 | 1 Trả lời
-
23/11/2022 | 1 Trả lời
-
a) Tính gia tốc của ô tô.
b) Tính vận tốc ô tô đạt được sau 40 s.
c) Sau bao lâu kể từ khi tăng tốc, ô tô đạt vận tốc 72 km/h.
23/11/2022 | 1 Trả lời
-
A. Viên bi lăn xuống trên máng nghiêng.
B. Vật rơi từ trên cao xuống đất.
C. Hòn đá bị ném theo phương nằm ngang.
D. Quả bóng được ném lên theo phương thẳng đứng.
23/11/2022 | 1 Trả lời
-
A. \({v^2} - v_{_0}^2 = ad.\)
B.\({v^2} - v_{_0}^2 = 2ad\)
C. \(v - {v_0} = 2ad\)
D.\({v_0}^2 - {v^2} = 2ad\)
24/11/2022 | 1 Trả lời
-
.png)
23/11/2022 | 1 Trả lời
-
A. Độ dịch chuyển giảm đều theo thời gian.
B. Vận tốc giảm đều theo thời gian.
C. Gia tốc giảm đều theo thời gian.
D. Cả 3 tính chất trên.
23/11/2022 | 1 Trả lời
-
.png)
a) Chuyển động của ô tô khi thấy đèn giao thông chuyển sang màu đỏ.
b) Chuyển động của vận động viên bơi lội khi có tín hiệu xuất phát.
c) Chuyển động của vận động viên bơi lội khi bơi đều.
d) Chuyển động của xe máy đang đứng yên khi người lái xe vừa tăng ga.
24/11/2022 | 1 Trả lời
-
a) Tính thời gian ngắn nhất để máy bay dừng hẳn kể từ khi tiếp đất.
b) Máy bay này có thể hạ cánh an toàn ở sân bay có đường bay dài 1 km hay không?
23/11/2022 | 1 Trả lời
-
23/11/2022 | 1 Trả lời
-
23/11/2022 | 1 Trả lời
-
A. Một chiếc khăn voan nhẹ.
B. Một sợi chỉ.
C. Một chiếc lá cây rụng.
D. Một viên sỏi.
23/11/2022 | 1 Trả lời
-
A. Chuyển động của một viên bi sắt được ném theo phương nằm ngang.
B. Chuyển động của một viên bi sắt được ném theo phương xiên góc.
C. Chuyển động của một viên bi sắt được thả rơi.
D. Chuyển động của một viên bi sắt được ném lên cao.
23/11/2022 | 2 Trả lời
-
24/11/2022 | 1 Trả lời
-
A. v = \(2\sqrt {gh} .\) B. v = \(\sqrt {2gh} .\)
C. v = \(\sqrt {gh} .\) D. \(\sqrt {\frac{{gh}}{2}} .\)
23/11/2022 | 1 Trả lời



