-
Câu hỏi:
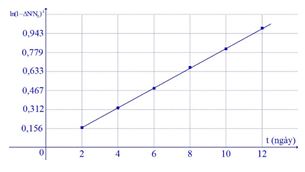
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?
-
A.
\(5,6\) ngày
-
B.
\(8,9\) ngày
-
C.
\(3,8\) ngày
-
D.
\(138\) ngày
Lời giải tham khảo:
Đáp án đúng: B
Đáp án : B
Ta có: \(N = {N_0}{e^{ - \lambda t}} \Rightarrow \)Số hạt bị phân rã là:
\(\Delta N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}(1 - {e^{ - \lambda t}})\)
\( \Rightarrow \dfrac{{\Delta N}}{{{N_0}}} = 1 - {e^{ - \lambda t}} \Rightarrow 1 - \dfrac{{\Delta N}}{{{N_0}}} = {e^{ - \lambda t}}\)
\( \Rightarrow \dfrac{1}{{\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)}} = {e^{\lambda t}} \Rightarrow \ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\)
Từ đồ thị ta thấy \(\lambda \approx 0,078\)
\( \Rightarrow T = \dfrac{{\ln 2}}{\lambda } \approx 8,9\) (ngày)
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Khi nói về ánh sáng đơn sắc, phát biểu nào dưới đây sai?
- Cho một vật dao động điều hòa với phương trình \(x = A\cos (\omega t + \varphi )\), giá trị cực tiểu của vận tốc là
- Hãy cho biết. Dao động của con lắc đồng hồ là
- Hãy cho biết. Sóng cơ học lan truyền trong không khí với cường độ đủ lớn, tai ta có thể cảm thụ được sóng cơ học nào?
- Đặt một điện áp xoay chiều vào hai đầu đoạn mạch chỉ có tụ điện thì
- Hãy cho biết. Theo thuyết lượng tử ánh sáng, phát biểu nào dưới đây là sai?
- Trong các hạt nhân nguyên tử: \(_{\rm{2}}^{\rm{4}}{\rm{He; }}_{{\rm{26}}}^{{\rm{56}}}{\rm{Fe; }}_{{\rm{92}}}^{{\rm{238}}}{\rm{U}}\) và \(_{{\rm{90}}}^{{\rm{230}}}{\rm{Th,}}\) hạt nhân bền vững nhất là
- Hãy cho biết. Tia hồng ngoại được dùng
- Hãy cho biết. Giảm xóc của ô tô là áp dụng của
- Hãy cho biết. Trong hiện tượng giao thoa sóng trên mặt nước, khoảng cách giữa hai cực đại liên tiếp nằm trên đường nối hai nguồn
- Cho phản ứng hạt nhân \(_{\rm{0}}^{\rm{1}}{\rm{n + }}_{{\rm{92}}}^{{\rm{235}}}{\rm{U}} \to _{{\rm{38}}}^{{\rm{94}}}{\rm{Sr + X + 2}}_{\rm{0}}^{\rm{1}}{\rm{n}}.\) Hạt nhân X có cấu tạo gồm:
- Gọi năng lượng của photon ánh sáng đỏ, ánh sáng lục và ánh sáng tím lần lượt là \({{\rm{\varepsilon }}_{\rm{D}}}{\rm{, }}{{\rm{\varepsilon }}_{\rm{L}}}\) và \({{\rm{\varepsilon }}_{\rm{T}}}\) thì
- Đặt điện áp xoay chiều \(u = {U_0}\cos \omega t\) vào hai đầu đoạn mạch chỉ có điện trở thuần. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch; i, I0 và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch. Hệ thức nào sau đây sai?
- Một sóng âm và một sóng ánh sáng truyền từ nước ra không khí thì bước sóng
- Sợi dây \(AB = 21 cm\) với đầu B tự do gây ra tại A một sóng ngang có tần số \(f\). Tốc độ truyền sóng trên dây là \(v = 4 m/s\), muốn có \(8\) bụng sóng thì tần số dao động phải là bao nhiêu?
- Để truyền thông tin liên lạc bằng sóng vô tuyến, người ta sử dụng phương pháp biến điệu biên độ, trong đó sóng cao tần có tần số \(800 kHz\) và sóng âm tần có tần số \(1 kHz\). Tần số của sóng sau khi biến điệu là
- Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tư cảm \(L\) và tụ điện có điện dung \(C\) đang có dao động điện từ tự do. Ở thời điểm \(t\), dòng điện qua cuộn dây có cường độ bằng \(0\) thì ở thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2}\)
- Máy phát điện xoay chiều một pha, phần cảm là nam châm điện có n cặp cực từ. Khi roto quay với tốc độ 600 vòng/phút thì máy tạo ra suất điện động \({\rm{e}} = 1{\rm{000}}\sqrt {\rm{2}} {\rm{cos(100\pi t) (V)}}\). Số cặp cực từ là
- Một sóng ngang truyền trên bề mặt với tần số \(f = 10 Hz\). Tại một thời điểm nào đó một phần tử mặt cắt của nước có hình dạng như hình vẽ. Trong đó khoảng cách từ vị trí cân bằng của \(A\) đến vị trí cân bằng của \(D\) là \(60 cm\) và điểm \(C\) đang đi xuống qua vị trí cân bằng. Chiều truyền sóng và tốc độ truyền sóng là
- Để xác định độ tự cảm \(L\) và điện trở trong \(r\) của một cuộn dây, một học sinh mắc nối tiếp điện trở \({\rm{R = 10 \Omega }}\) với cuộn dây như hình (hình a). Dùng vôn kế đo các điện áp trên mạch với các vị trí \(U_{ab}\), \(U_{bc}\), \(U_{ac}\), sau đó giản đồ Frenen với các véc-tơ tương ứng theo đúng tỉ lệ như hình (hình b). Độ tự cảm và điện trở trong của cuộn dây trong thí nghiệm này gần giá trị nào nhất? Biết tần số góc của mạch \(\omega =100\pi (rad/s)\)
- Hạt \(\alpha \) bắn vào hạt nhân Al đứng yên gây ra phản ứng: \(_{13}^{27}Al + \alpha \to _{15}^{30}P + n\). Phản ứng này thu năng lượng \(Q = 2,7 MeV\). Biết hai hạt sinh ra có cùng vận tốc. Coi khối lượng hạt nhân bằng số khối của chúng. Động năng của hạt \(\alpha \) là
- Một học sinh thực hiện thí nghiệm khảo sát ảnh hưởng của chiều dài con lắc đơn với chu kì dao động kiểm chứng chu kì dao động. Từ kết quả thí nghiệm, học sinh này vẽ đồ thị biểu diễn sự phụ thuộc của \(T^2\) vào chiều dài \(l\)) của con lắc như hình vẽ. Góc \({\rm{\alpha }}\) đo được trên hình bằng 76,10. Lấy \(\pi \approx 3,14\). Theo kết quả thí nghiệm của học sinh này thì gia tốc trọng trường tại nơi làm thí nghiệm là
- Dòng điện cảm ứng IC trong vòng dây có chiều như hình vẽ. Nhận xét nào sau đây đúng?
- Một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm không đổi, tụ điện có điện dung \(C\) thay đổi. Khi \(C = C_1\) thì tần số dao động riêng của mạch là \(7,5 MHz\) và khi \(C = C_2\) thì tần số dao động riêng của mạch là \(10,0 MHz\). Nếu \(C = C_1+ C_2\) thì tần số dao động riêng của mạch là
- Để xác định điện trở trong r của một nguồn điện, một học sinh mắc mạch điện như hình (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của số chỉ U của vôn kế V vào số chỉ I của ampe kế A như hình (H2). Điện trở của vôn kế rất lớn. Biết \({R_0} = 2{\rm{0,3 \Omega }}\). Giá trị của r được xác định bởi thí nghiệm này là
- Hãy cho biết. Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, \(k = 50 N/m\), \(m = 200 g\).
- Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết \({r_2} = \dfrac{{{r_1} + {r_3}}}{2}\)và các điểm cùng nằm trên một đường sức. Giá trị của x bằng
- Cho mạch điện như hình vẽ, bỏ qua điện trở của dây nối, biết \(E = 3 V\),\({R_1} = 5\Omega \) ampe kế chỉ \(0,3 A\), vôn kế chỉ \(1,2 V\). Ampe kế và vôn kế lí tưởng. Giá trị điện trở trong \(r\) của nguồn là
- Trong thí nghiệm giao thoa ánh sáng nhìn thấy dùng khe I-âng, có khoảng cách 2 khe là \(a = 2 mm\), từ màn ảnh đến 2 khe là \(D = 1m\). Chiếu đồng thời 2 bức xạ \({\lambda _1}\) và \({\lambda _2}\)(\({\lambda _2} > {\lambda _1})\)thì vân sáng bậc 3 của bức xạ \({\lambda _1}\) trùng với vân sáng bậc k của bức xạ \({\lambda _2}\) và cách vân trung tâm \(0,6 mm\). Hỏi \(k\) và \({\lambda _2}\) bằng bao nhiêu?
- Trong hình vẽ bên, S’ là ảnh của một điểm sáng S qua một thấu kình có trục chính xx’. Nhận xét nào sau đây sai?
- Mắc vào đoạn mạch RLC không phân nhánh gồm một nguồn điện xoay chiều có tần số thay đổi được. Ở tần số \({f_1} = {\rm{60 Hz,}}\) hệ số công suất đạt cực đại. Ở tần số \({f_2} = 120{\rm{ Hz,}}\) hệ số công suất nhận giá trị \(\cos {\rm{\varphi }} = \dfrac{1}{{\sqrt 2 }}\). Ở tần số \({f_3} = 90{\rm{ Hz,}}\) hệ số công suất của mạch sẽ nhận giá trị
- Điện năng từ một trạm phát điện được đưa đến khu tái định cư bằng đường dây truyền tải một pha. Biết rằng nếu điện áp tại nơi truyền tải tăng từ \(U\) đến \(2U\) thì số hộ dân được trạm phát cung cấp đủ điện năng tăng từ \(120\) hộ đến \(156\) hộ. Coi rằng công suất tiêu thụ điện mỗi hộ là không đổi, hệ số công xuất nơi truyền tải không đổi. Để trạm phát phục vụ đủ \(165\) hộ dân thì điện áp nơi phát là
- Hai con lắc lò xo giống hệt nhau được treo thẳng đứng, sát nhau trên cùng một giá cố định nằm ngang. Mỗi con lắc gồm lò xo nhẹ độ cứng k và một vật nhỏ có khối lượng 125 g. Kích thích cho hai vật dao động điều hòa sao cho biên độ dao động thỏa mãn \({A_1} + {A_2} = {\rm{8 (cm)}}\). Tại mọi thời điểm li độ và vận tốc của các vật liên hệ với nhau bằng biểu thức: \({v_2}{x_1} + {v_1}{x_2} = 96\pi ;\)v(cm/s); x(cm). Bỏ qua mọi ma sát, lấy \(g = 1{\rm{0 (m/}}{{\rm{s}}^{\rm{2}}}{\rm{), }}{\pi ^2} = 10.\) Độ cứng k của lò xo không thể nhận giá trị nào sau đây?
- Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?
- Trong giờ thực hành vật lí có sử dụng bộ thí nghiệm điện xoay chiều Vật lí 12 để tiến hành lắp mạch điện. Bảng lắp ráp mạch điện được vẽ lại như hình vẽ, với các chốt cắm có tên tương ứng. Một học sinh lắp mạch như sau: giữa E, C lắp cuộn cảm thuần có độ tự cảm \(31,85 mH\);
- Công thoát electron của một kim loại là \(4,775 eV\). Chiếu lần lượt vào bề mặt tấm kim loại này các bức xạ có bước sóng là \({{\rm{\lambda }}_{\rm{1}}}{\rm{ = 0,18 \mu m, }}{{\rm{\lambda }}_{\rm{2}}}{\rm{ = 0,21 \mu m}}\) và \({{\rm{\lambda }}_{\rm{3}}}{\rm{ = 0,35 \mu m}}.\) Bức xạ nào gây được hiện tượng quang điện đối với kim loại đó?
- Một con lắc lò xo dao động trên trục Ox, gọi \({\rm{\Delta t}}\) là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng. Tại thời điểm t vật đi qua vị trí có tốc độ \(15\pi \sqrt 3 \)cm/s với độ lớn gia tốc \(22,5 m/s^2\), sau đó một khoảng thời gian đúng bằng \({\rm{\Delta t}}\) vật đi qua vị trí có độ lớn vận tốc \(45\pi cm/s\). Lấy \({\pi ^2} = 10.\) Biên độ dao động của vật là
- Hãy cho biết. Trong chùm tia Rơn-ghen phát ra từ một ống Rơn-ghen, người ta thấy những tia có tần số lớn nhất bằng \({f_{\max }} = {3.
- Tại điểm \(O\) đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm \(A\) cách \(O\) một đoạn \(d\) (\(m\)) có mức cường độ âm là \(L_A = 40 dB\). Trên tia vuông góc với \(OA\) tại \(A\), lấy điểm \(B\) cách \(A\) một khoảng \(6 m\). Điểm \(M\) thuộc đoạn \(AB\) sao cho \(AM = 4,5 m\) và góc \(\widehat {MOB}\)có giá trị lớn nhất. Để mức cường độ âm tại \(M\) là \(50 dB\) thì cần đặt thêm tại \(O\) bao nhiêu nguồn âm nữa?
- Lần lượt đặt vào hai đầu đoạn mạch xoay chiều RLC không phân nhánh (\(R\) là biến trở, \(L\) thuần cảm) hai điện áp xoay chiều \({u_1} = {U_{01}}\cos ({\omega _1}t + {\varphi _1})\) và \({u_2} = {U_{02}}\cos ({\omega _2}t + {\varphi _2})\) người ta thu được đồ thị công suất của mạch điện xoay chiều theo biến trở \(R\) như hình vẽ (đường 1 là của \(u_1\) và đường 2 là của \(u_2\)).