-
Câu hỏi:
Hình vuông có đường chéo bằng \(2\,dm\) thì cạnh bằng:
-
A.
\(\frac{3}{2}\,dm\)
-
B.
\(1\,dm\)
-
C.
\(\sqrt 2 \,dm\)
-
D.
\(2\,dm\)
Lời giải tham khảo:
Đáp án đúng: C
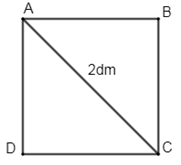
Xét hình vuông \(ABC{\rm{D}}\) có độ dài đường chéo\(AC = 2\,dm\) .
Áp dụng định lí py-ta-go cho \({\Delta _v}A{\rm{D}}C\) có:
\(A{{\rm{D}}^2} + D{C^2} = A{C^2} \Rightarrow 2A{{\rm{D}}^2} = {2^2} \Rightarrow A{{\rm{D}}^2} = 2 \Rightarrow A{\rm{D}} = \sqrt 2 dm\)
Vậy cạnh của hình vuông đó bằng \(1\,dm\) .
Chọn C
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Kết quả của phép tính \(8{x^2}:4x\) là
- Cho biết biểu thức \({x^2} - {y^2}\) bằng:
- Phân tích đa thức \(x{y^2} + 2xy + x\) ta được
- Tổng của hai phân thức \(\frac{3}{{7xy}} + \frac{4}{{7xy}}\) là
- Hình nào đã cho dưới đây không có tâm đối xứng?
- Hình thang cân là:
- Cho tam giác vuông như hình vẽ: Diện tích của tam giác bằng:
- Tìm kết quả phép tính: \(2x.(3{x^2} + 1)\)
- Tìm \(x\) biết: \({x^2} + 5x = 0\)
- Phân tích đa thức sau thành nhân tử: \({x^2} - 2x - xy + 2y\).
- Tìm giá trị nhỏ nhất của \(A = {x^2} - 2x + 3\) với mọi số thực \(x \in Z\).
- Tìm giá trị nguyên của \(n\) để \(({n^3} - 3{n^2} + n)\,\, \vdots \,\,(n - 3)\).
- Phép nhân \(5x(3{x^2} - 4x + 2)\) được kết quả là
- Thực hiện phép chia \(\left( {{x^2} + 2017x} \right):\left( {x + 2017} \right)\) ta được kết quả là
- Chọn câu phát biểu sai về các hình? Chọn câu phát biểu sai?
- Nếu tăng độ dài của một hình vuông lên \(3\) lần thì diện tích hình vuông đó tăng lên mấy lần?
- Tính giá trị của biểu thức \(B = {x^2} + 2x + 1 + {y^2} - 4y + 4\) tại \(x = 99\) và \(y = 102\).
- Phân tích đa thức sau thành nhân tử: \(2{x^2} - 2{y^2} + 16x + 32\).
- Tìm \(x\) biết: \({x^2} - 3x + 2x - 6 = 0\).
- Rút gọn phân thức: \(P = \frac{{9 - {x^2}}}{{{x^2} - 3x}}\).
- Thực hiện phép tính: \(\frac{{{x^2}}}{{{x^2} + 2x + 1}} - \frac{1}{{{x^2} + 2x + 1}} + \frac{2}{{x + 1}}\).
- Hình vuông có độ dài đường chéo là \(6cm\). Độ dài cạnh hình vuông đó là:
- Một hình chữ nhật có diện tích \(15{m^2}\). Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là:
- Đa thức \(12x - 36 - {x^2}\) bằng:
- Kết quả của phép cộng: \(\frac{{3x - 1}}{{3x - 3}} + \frac{{ - 2}}{{3x - 3}}\) là:
- Kết quả rút gọn biểu thức:\(\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) - \left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right)\) là:
- Số dư khi chia đa thức: \(3{x^4} - 2{x^3} + {x^2} - 2x + 2\) cho đa thức \(x - 2\) là:
- Cho hình thang cân \(ABC{\rm{D}}\,\left( {AB//C{\rm{D}}} \right)\) có \(\angle A = {135^0}\) thì \(\angle C\) bằng:
- Tứ giác có các đỉnh là trung điểm các cạnh của một tứ giác có hai đường chéo bằng nhau là:
- Tính giá trị của biểu thức: \(\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)\left( {1 - \frac{1}{{{4^2}}}} \right)...\left( {1 - \frac{1}{{{{2017}^2}}}} \right)\)
- Hình vuông có đường chéo bằng \(2\,dm\) thì cạnh bằng:
- Hình thoi có hai đường chéo bằng \(6\,cm\) và \(8\,cm\) thì cạnh bằng:
- Phân thức: \(\frac{{{x^2} - 2017}}{{1 + {x^{2018}}}}\) xác định với:
- Kết quả của phép tính: \(\left( {{a^2} + 2a + 4} \right)\left( {a - 2} \right)\) là:
- Phân tích đa thức \({x^2} - x - 6\) thành nhân tử được kết quả là:
- Hình chữ nhật \(ABC{\rm{D}}\) có \(AB = 6\,cm,\,BC = 4\,cm\). Khi đó, diện tích hình chữ nhật ABCD là:
- Số lượng trục đối xứng của hình vuông là:
- Tập hợp tất cả các giá trị của \(x\) thỏa mãn: \({x^3} = - x\) là:
- Một hình thoi có cạnh bằng \(10\,cm\)và độ dài một đường chéo là \(12\,cm\). Khi đó, độ dài đường chéo còn lại của hình thoi là:
- Tứ giác là hình vuông khi tứ giác đó có:

