-
Câu hỏi:
Cho tam giác ABC ngoại tiếp đường tròn (O). Biết \(\widehat{AOC}=130^o, \widehat{OCA}=30^o\). So sánh OB và OC
-
A.
OB<OC
-
B.
OB>OC
-
C.
OB=OC
-
D.
Chưa đủ dữ kiện để so sánh
Lời giải tham khảo:
Đáp án đúng: A
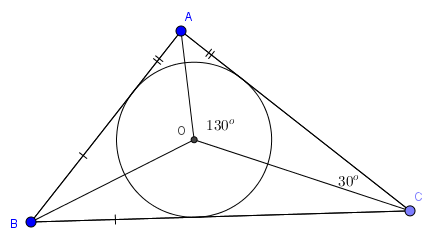
Ta có: \(\widehat{OAC}=180-130-30=20\Rightarrow \widehat{BAC}=40^o\Rightarrow \widehat{ABC}=80^o\) \(\Rightarrow \widehat{OBC}=40^o\)
Xét tam giác OBC có: \(\widehat{OBC}=40^o>30^o=\widehat{OCB}\Rightarrow OC>OB\)
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
QUẢNG CÁO
CÂU HỎI KHÁC
- Cho đường tròn (O). M là điểm ngoài đường tròn, vẽ hai tiếp tuyến MA, MB của (O). Khẳng định nào sau đây là sai
- Phát biểu nào sau đây là đúng
- Cho tam giác ABC vuông tại A có AB=3, AC=4. Đường tròn (I;r) nội tiếp tam giác ABC. Giá trị của r là:
- Cho tam giác ACB vuông tại A. O là tâm đường tròn nội tiếp tam giác ABC. D, E, F lần lượt là các tiếp điểm trên AB, AC, BC. Hệ thức nào đúng
- Cho tam giác ABC ngoại tiếp đường tròn (O). Biết widehat{AOC}=130^o, widehat{OCA}=30^o. So sánh OB và OC
VIDEO
YOMEDIA
