Giải Bài tập 12.5 trang 20 SBT Vật lý 10 Kết nối tri thức
Một vật được ném theo phương nằm ngang từ độ cao 4,9 m, có tầm xa trên mặt đất L= 5 m. Lấy g= 9,8 m/s2
a) Tính vận tốc ban đầu.
b) Viết phương trình chuyển động và vẽ đồ thị độ dịch chuyền – thời gian.
c) Xác định vận tốc của vật ngay trước khi chạm đất.
Hướng dẫn giải chi tiết Bài tập 12.5
Phương pháp giải:
a) Áp dụng công thức tính tầm xa của vật bị ném: L = v0\(\sqrt {\frac{{2H}}{g}} \).
b) Xác định độ dịch chuyển theo phương thẳng đứng y và độ dịch chuyển theo phương nằm ngang x.
c) Sử dụng công thức tổng hợp vận tốc: v2 = vx2 + vy2
Trong đó: vx = v0; vy = gt.
Lời giải chi tiết:
a) Theo công thức tính tầm xa của vật bị ném: L = v0\(\sqrt {\frac{{2h}}{g}} \)
=> v0 = L\(\sqrt {\frac{g}{{2h}}} \)= 5\(\sqrt {\frac{{9,8}}{{2.4,9}}} \)= 5 m/s.
b) Ta cần xác định được mối quan hệ giữa độ dịch chuyển theo phương thẳng đứng y và độ dịch chuyển theo phương nằm ngang x:
Ta có: x = v0t => t = \(\frac{x}{{{v_0}}}\);
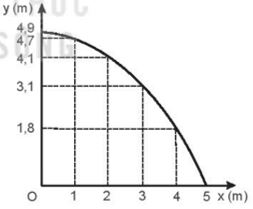
y = h = \(\frac{1}{2}\)gt2 = 4,9 - \(\frac{1}{2}\)g\(\frac{{{x^2}}}{{v_0^2}}\)= 4,9 – 0,196x2
Ta lập bảng biến thiên với 6 giá trị của x và y:
Quỹ đạo là \(\frac{1}{2}\)đường parabol như hình vẽ:
c) Ta có vx = v0 = 5 m/s;
vy = gt = g\(\sqrt {\frac{{2h}}{g}} \)= \(\sqrt {2gh} \)= \(\sqrt {2.9,8.4,9} \)= 9,8 m/s.
Do đó: v =\(\sqrt {{v_x}^2 + {\rm{ }}{v_y}^2} \) =\(\sqrt {{5^2} + {\rm{ 9,}}{{\rm{8}}^2}} \)≈ 11m/s.
Ta có: tanα = \(\frac{{{v_y}}}{{{v_x}}}\) = 1,96 => α ≈ 63o.
Vậy vận tốc của vật ngay trước khi chạm đất có độ lớn là 11 m/s, hướng xuống dưới 63o so với phương nằm ngang.
-- Mod Vật Lý 10 HỌC247
Bài tập SGK khác
Giải Bài tập 12.3 trang 19 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.4 trang 19 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.6 trang 20 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.7 trang 20 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.8 trang 20 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.9 trang 20 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.10 trang 20 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.11 trang 21 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.12 trang 21 SBT Vật lý 10 Kết nối tri thức - KNTT
Giải Bài tập 12.13 trang 21 SBT Vật lý 10 Kết nối tri thức - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.