Câu hỏi thảo luận 3 trang 49 SGK Vật Lý 10 Chân trời sáng tạo
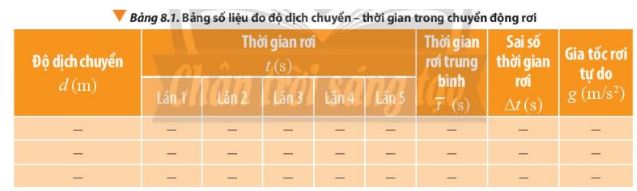
Dựa vào bảng số liệu, lập luận để trình bày phương án và tiến hành xử lí số liệu để xác định gia tốc rơi tự do và sai số của phép đo.
Hướng dẫn giải chi tiết Câu hỏi thảo luận 3
Phương pháp giải:
Quan sát bảng số liệu và áp dụng các kiến thức đã học để tính
Sai số tuyệt đối của phép đo ở mỗi độ dịch chuyển được tính theo công thức:
\(\Delta t = \Delta \bar t + \Delta {t_{dc}}\)
Lời giải chi tiết:
Tham khảo bảng số liệu dưới:
|
Độ dịch chuyển d (m) |
Thời gian rơi t (s) |
Thời gian rơi trung bình \(\bar t\) (s) |
Sai số thời gian rơi ∆t (s) |
Gia tốc rơi tự do g (m/s2) |
||||
|
Lần 1 |
Lần 2 |
Lần 3 |
Lần 4 |
Lần 5 |
||||
|
0,4 |
0,285 |
0,286 |
0,284 |
0,285 |
0,286 |
0,285 |
|
|
|
0,6 |
0,349 |
0,351 |
0,348 |
0,349 |
0,350 |
0,349 |
|
|
|
0,8 |
0,404 |
0,405 |
0,403 |
0,404 |
0,403 |
0,404 |
|
|
Thời gian rơi trung bình:
- Độ dịch chuyển 0,4 (m):
\(\bar t = \frac{{{t_1} + {t_2} + {t_3} + {t_4} + {t_5}}}{5} \approx 0,285\,s\)
- Độ dịch chuyển 0,6 (m):
\(\bar t = \frac{{{t_1} + {t_2} + {t_3} + {t_4} + {t_5}}}{5} \approx 0,349s\)
- Độ dịch chuyển 0,8 (m):
\(\bar t = \frac{{{t_1} + {t_2} + {t_3} + {t_4} + {t_5}}}{5} \approx 0,404s\)
Sai số tuyệt đối trung bình:
- Độ dịch chuyển 0,4 (m):
\(\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + \Delta {t_3} + \Delta {t_4} + \Delta {t_5}}}{5} \approx {6.10^{ - 4}}\,s\)
- Độ dịch chuyển 0,6 (m):
\(\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + \Delta {t_3} + \Delta {t_4} + \Delta {t_5}}}{5} \approx {8.10^{ - 4}}\,s\)
- Độ dịch chuyển 0,8 (m):
\(\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + \Delta {t_3} + \Delta {t_4} + \Delta {t_5}}}{5} \approx {6.10^{ - 4}}\,s\)
Ta chọn thang đo 9,999 s – 0,001 s thì ta có sai số dụng cụ ∆tdc = 0,0005s
Sai số tuyệt đối của phép đo ở mỗi độ dịch chuyển được tính theo công thức:
\(\Delta t = \Delta \bar t + \Delta {t_{dc}}\)
- Độ dịch chuyển 0,4 (m): ∆t = 1,1.10-3s
- Độ dịch chuyển 0,6 (m): ∆t = 1,3.10-3s
- Độ dịch chuyển 0,8 (m): ∆t = 1,1.10-3s
Gia tốc rơi tự do trung bình:
- Độ dịch chuyển 0,4 (m): \(\bar g = \frac{{2d}}{{{{\bar t}^2}}} \approx 9,85\,m/{s^2}\)
- Độ dịch chuyển 0,6 (m): \(\bar g = \frac{{2d}}{{{{\bar t}^2}}} \approx 9,85\,m/{s^2}\)
- Độ dịch chuyển 0,8 (m): \(\bar g = \frac{{2d}}{{{{\bar t}^2}}} \approx 9,80\,m/{s^2}\)
Sai số tương đối của gia tốc ở mỗi độ dịch chuyển được tính theo công thức:
\(\delta g = \frac{{2\Delta t}}{{\bar t}}.100\% \)
- Độ dịch chuyển 0,4 (m):
\(\delta g = \frac{{2.1,{{1.10}^{ - 3}}}}{{0,285}}.100\% \approx 0,008\% \)
- Độ dịch chuyển 0,6 (m):
\(\delta g = \frac{{2.1,{{1.10}^{ - 3}}}}{{0,349}}.100\% \approx 0,0074\% \)
- Độ dịch chuyển 0,8 (m):
\(\delta g = \frac{{2.1,{{1.10}^{ - 3}}}}{{0,404}}.100\% \approx 0,0054\% \)
Kết quả gia tốc được viết ở mỗi độ dịch chuyển là:
- Độ dịch chuyển 0,4 (m):
\(g = 9,85\,m/{s^2} \pm 0,008\% \)
- Độ dịch chuyển 0,6 (m):
\(g = 9,85\,m/{s^2} \pm 0,0074\% \)
- Độ dịch chuyển 0,8 (m):
\(g = 9,85\,m/{s^2} \pm 0,0054\% \)
-- Mod Vật Lý 10 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.