Bài tập 47 trang 163 SBT Toán 9 Tập 1
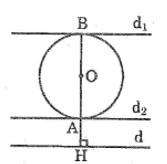
Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến của đường tròn (O) sao cho tiếp tuyến đó song song với d
Hướng dẫn giải chi tiết
* Phân tích
Giả sử tiếp tuyến của đường tròn dựng được thỏa mãn điều kiện bài toán
- d1 là tiếp tuyến của đường tròn tại A nên d1 ⊥ OA
- Vì d1 // d nên d ⊥ OA
Vậy A là giao điểm của đường thẳng kẻ từ O vuông góc với d
* Cách dựng
- Dựng OH vuông góc với d cắt đường tròn (O) tại A và B
- Dựng đường thẳng d1 đi qua A và vuông góc với OA
- Dựng đường thẳng d2 đi qua B và vuông góc với OB
Khi đó d1 và d2 là hai tiếp tuyến cần dựng.
* Chứng minh
Ta có: A và B thuộc (O)
d1 // d mà d ⊥ OH nên d1 ⊥ OH hay d1 ⊥ OA tại A
Suy ra d1 là tiếp tuyến của đường tròn (O)
d2 // d mà d ⊥ OH nên d2 ⊥ OH hay d2 ⊥ OB tại B
Suy ra d2 là tiếp tuyến của đường tròn (O)
* Biện luận
Đường thẳng OH luôn cắt đường tròn (O) nên giao điểm A và B luôn dựng được.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-
Chứng minh CB là tiếp tuyến của tâm O
bởi Đan Nguyên
26/01/2019
bài 1 : cho đg tròn tâm O dây AB khác đg kính . Qua O kẻ đt vuông góc AB cắt tiếp tuyến tại A tại A của đg tròn tâm C
a, Cmr : CB là tiếp tuyến của tâm O
b, biết R = 15cm , AB = 24cm . tính OC
BÀI 2 : Cho tg ABC có AB = 5cm , AC = 12cm , BC =13cm . VE đg tròn tâm B , R =5cm CMR : AC là tiếp tuyến của đg tròn tâm B
Theo dõi (0) 1 Trả lời -
Chứng minh NA, NB là các tiếp tuyến của (O)
bởi Truc Ly
29/01/2019
cho (O) . lấy N bất kì ngoài (O). trên (O) lấy A,B sao cho NA=NB; ON lần lượt là p/g các góc ANB và AOB. c/m NA,NB là các tiếp tuyến của (O)
Theo dõi (0) 1 Trả lời -
Bài 5.2 trang 164 sách bài tập toán 9 tập 1
bởi hành thư
10/10/2018
Bài 5.2 - Bài tập bổ sung (Sách bài tập trang 164)
Cho đường tròn (O) đường kính AB, dây CD vuông góc với OA tại trung điểm của OA. Gọi M là điểm đối xứng với O qua A. Chứng minh rừng MC là tiếp tuyến của đường tròn ?
Theo dõi (0) 1 Trả lời -
Bài 46 trang 163 sách bài tập toán 9 tập 1
bởi Lê Tấn Thanh
10/10/2018
Bài 46 (Sách bài tập trang 163)Cho góc nhọn xOy, điểm A thuộc tia Ox. Dựng đường tròn tâm I tiếp xúc với Ox tại A và có tâm I nằm trên tia Oy ?
Theo dõi (0) 1 Trả lời
