Bài tập 47 tr 108 sách BT Toán lớp 9 Tập 2
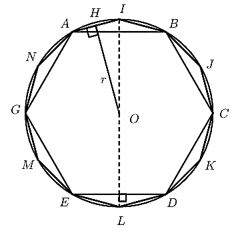
\(a)\) Vẽ một lục giác đều \(ABCDEG\) nội tiếp đường tròn bán kính \(2cm\) rồi vẽ hình \(12\) cạnh đều \(AIBJCKDLEMGN\) nội tiếp đường tròn đó. Nêu cách vẽ.
\(b)\) Tính độ dài cạnh \(AI.\)
\(c)\) Tính bán kính \(r\) của đường tròn nội tiếp hình \(AIBJCKDLEMGN.\)
Hướng dẫn. Áp dụng các công thức ở bài \(46.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều \(n\) cạnh bằng \(\dfrac{360^\circ}{n}.\)
Lời giải chi tiết
\(a)\) Cách vẽ:
− Vẽ đường tròn \((0; 2cm)\)
− Từ điểm \(A\) trên đường tròn \((0; 2cm)\) đặt liên tiếp các cung bằng nhau có dây căng cung \(2cm.\)
\(\overparen{AB}\) \( =\overparen{BC}\) \( =\overparen{CD}\) \( =\overparen{DE}\) \( =\overparen{EG}\)
Nối \(AB, BC, CD, DE, EG, GA\) ta có lục giác đều \(ABCDEG\) nội tiếp trong đường tròn \((0; 2cm).\)
− Kẻ đường kính vuông góc với \(AB\) và \(DE\) cắt đường tròn tại \(I\) và \(L.\)
Ta có: \(\overparen{AI}= \overparen{IB};\) \(\overparen{LD} =\overparen{LE}\)
− Kẻ đường kính vuông góc với \(BC\) và \(EG\) cắt đường tròn tại \(J\) và \(M.\)
\(\overparen{BJ} = \overparen{JC}\); \(\overparen{ME} = \overparen{MG}\)
− Kẻ đường kính vuông góc với \(CD\) và \(AG\) cắt đường tròn tại \(N\) và \(K.\)
\(\overparen{KC}= \overparen{KD};\) \(\overparen{NA} = \overparen{NG}\)
Nối \(AI, IB, BJ, JC, CK, KD, DL,\) \(LE,\) \(EM,\) \(MG,\) \(GN,\) \(NA\)
Ta có đa giác đều \(12\) cạnh \(AIBJCKDLEMGN.\)
\(b)\) \(AI\) là cạnh của đa giác đều \(12\) cạnh.
Kẻ \(OH ⊥ AI\)
\(\widehat {IOH} = \displaystyle{{180^\circ } \over {12}} = 15^\circ \)
Xét tam giác vuông \(IOH\) có: \(OI = \displaystyle{{HI} \over {\sin \widehat {IOH}}} \)
\(\Rightarrow OI = \displaystyle{{AI} \over {2\sin \widehat {IOH}}}\)
\(\Rightarrow AI = OI.2\sin \widehat {IOH}\)
\(AI = 2. 2sin15^\circ \approx \)\( 1,04 (cm)\)
\(c)\) \(OH = r\) bán kính đường tròn nội tiếp đa giác đều \(12\) cạnh.
Trong tam giác vuông \(OHI\) ta có \(OH = OI.{\rm{cos}}\widehat {HOI} = 2.c{\rm{os15}}^\circ \approx {\rm{1,93 (cm) }}\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-
Chứng minh tam giác EBF cân
bởi Hoa Lan
16/01/2019
Cho tam giác abc vuông tại a (AB<AC). Nội tiếp đường tròn tâm O đường kính BC. Kẻ dây AD vuông góc với BC. Gọi CA giao BD tại E. Qua E kẻ đường thẳng vuông góc với CB ở H., AB ở F. Chứng minh:
a, tam giác EBF cân.
b, Tam giác HAE cân.
c, HA là tiếp tuyến Của tâm O
Theo dõi (0) 1 Trả lời -
Chứng minh rằng OA⊥BC và DC//OA
bởi Phạm Khánh Ngọc
16/01/2019
Cho đường tròn(O,R) và 1 điểm A nằm ngoài đường tròn. Từ A vẽ 2 tiếp tuyến AB và AC ( B,C là tiếp điểm). Kẻ đường kính BD, đường thẳng vuong góc với BD tại O cắt đường thẳng DC tại E
a)C/m: OA\(\perp\)BC và DC//OA
b) C/m AEDO là hình bình hành
c) Đường thẳng BC cắt OA và OE lần lượt tại I và K. C/m IK.IC+OA.OI=\(R^2\)
Theo dõi (0) 1 Trả lời -
Chứng minh 5 điểm A,B,I,C,O cùng nằm trên 1 đường tròn
bởi con cai
16/01/2019
Từ 1 điểm A ở ngoài đường tròn (O) vẽ 2 tiếp tuyến AB , AC và cát tuyến AMN của đường tròn đó . Gọi I là trung điểm của dây MN , H là giao điểm của AO và BC . Chứng minh
a, 5 điểm A,B,I,C,O cùng nằm trên 1 đường tròn
b, AB2 = AM.AN và \(\widehat{AHM}\) = \(\widehat{ANO}\)
Theo dõi (0) 1 Trả lời -
Chứng minh rằng MC.MD = MO^2 - R^2
bởi Anh Nguyễn
16/01/2019
Cho đường tròn (O) có MA, MB là tiếp tuyến , MCD là các tuyến
C/minh
MC.MD = MO2 - R2
Theo dõi (0) 1 Trả lời -
ADMICRO
Chứng minh rằng AMON là tứ giác nội tiếp
bởi nguyen bao anh
16/01/2019
Từ A nằm ngoài (O) vẽ tiếp tuyến AM,AN cát tuyến ABC ( AC nằm giữa AO,AN). H là giao điểm của AD,MN
a) AMONlà tứ giắc nội tiếp
b) AH.AO=AB.AC
c) OHBC là tứ giác nội tiếp
d) từ M kẻ đường thẳng song song với AC cắt (O) tại I, tia IM cắt BC tại K. Cm : BK=CK
Theo dõi (0) 1 Trả lời -
Giải phương trình sau x+căn(x+1/2 căn(x+1/4))=2
bởi Choco Choco
16/01/2019
Giải phương trình sau:
x + \(\sqrt{x+\dfrac{1}{2}\sqrt{x+\dfrac{1}{4}}}\)=2
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC vuông tại C. Vẽ (O) đường kính AB. CMR: C thuộc đường tròn tâm O, bán kính AB/2
Theo dõi (0) 1 Trả lời -
cho tam giác ABC vuông tại A . Lấy điểm D trên cạnh AC sao cho AC > 2CD. Vẽ đường tròn tâm D tiếp xúc với BC tại E. Từ B kẻ tiếp tuyến thứ 2 BF ,cắt AD tại I và cắt AE tại K . Trung tuyến AM của tam giác ABC cắt BF tại N
a) chứng minh rằng 5 điểm A,B ,E,D,F cùng thuộc một đường tròn
b) chứng minh \(\dfrac{IF}{IK}\) = \(\dfrac{BF}{BK}\)
c) cho góc AEC = 130 . Tính góc ANB
Theo dõi (0) 1 Trả lời -
Chứng minh rằng MC là tiếp tuyến của (O)
bởi Co Nan
18/01/2019
cho đường tròn tâm O đường kính AB láy điểm C thuộc (O) tiếp tuyến A của (O) Tại D1gọi M Là trung điểm của AD
a/ Cmr : mc là tiếp tuyến của (O)
b/Cmr : MO vuông góc với AC tại trung điểm I của AC
c/ cho BC=R tính độ dài AC và số đoc góc ABC
d/Khi C chuyển động trên (O) chứng minh I thuộc đường tròn cố định
Theo dõi (0) 1 Trả lời -
Chứng minh rằng điểm E chia AB và CD thành những đoạn thẳng bằng nhau từng đôi một
bởi Tay Thu
18/01/2019
Cho 2 dây AB=CD cắt nhau tại E trong đường tròn (O). Chứng minh rằng điểm E chia AB và CD thành những đoạn thẳng bằng nhau từng đôi một
Theo dõi (0) 1 Trả lời -
Chứng minh C,D,E,F,M cùng thuộc một đường tròn
bởi bich thu
18/01/2019
Cho hình chữ nhật ABCD có AB=2AD.Gọi M là trung điểm của AB, E là hình chiếu vuông góc của C trên BD , F là hình chiếu vuông góc của D trên AC.
a) Chứng minh C,D,E,F,M cùng thuộc một đường tròn.
b) Tứ giác ABEF là hình gì ? Hỏi có đường tròn nào đi qua bốn điểm A,B,E,F ko?Theo dõi (0) 1 Trả lời -
Chứng minh rằng PA.PM=PB.PN
bởi Hương Lan
18/01/2019
Cho đường tròn (O) đường kính AB. 1 điểm P bên ngoài (O) và PA,PB lần lượt cắt đường tròn tại M và N.
a)Cm: PA.PM=PB.PN
b) Gọi H là giao điểm của AN và BM. Cm: PH vuông góc ABTheo dõi (0) 1 Trả lời -
Chứng minh góc ADE = góc ABC
bởi thuy linh
16/01/2019
Cho tam giác ABC nhọn nội tiếp (O) , đuoefng cao BE , CF cắt nhau tại H . Chứng minh góc ADE = góc ABC
Theo dõi (0) 1 Trả lời
