Giải bài 23 tr 119 sách GK Toán 9 Tập 2
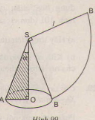
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc \(\small \alpha\) của tam giác vuông AOS- hình 99) sao cho diện tích khai triển mặt nón bằng một phần tư diện tích hình tròn (bán kính SA).
Hướng dẫn giải chi tiết bài 23
.png)
Diện tích hình quạt : \(S_{quạt} = \dfrac{\pi r^2 n^o}{360^o}= \dfrac{\pi.l^2.90}{360}=\dfrac{\pi.l^2}4.\)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\)
Theo đề bài ta có: \({S_{xq}} = S_{quạt} \Rightarrow πrl= \dfrac{\pi.l^2}4\)\(\Rightarrow\) \(l = 4r.\)
Trong tam giác vuông SOA, ta có: \(\sin \alpha =\dfrac {OA}{SA}= \dfrac{r}l = \dfrac {1}4\) (vì \(l=4r\).)
Vậy \(\alpha= {14^0}28'.\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 21 trang 118 SGK Toán 9 Tập 2
Bài tập 22 trang 118 SGK Toán 9 Tập 2
Bài tập 24 trang 119 SGK Toán 9 Tập 2
Bài tập 25 trang 119 SGK Toán 9 Tập 2
Bài tập 26 trang 119 SGK Toán 9 Tập 2
Bài tập 27 trang 119 SGK Toán 9 Tập 2
Bài tập 28 trang 120 SGK Toán 9 Tập 2
Bài tập 29 trang 120 SGK Toán 9 Tập 2
Bài tập 14 trang 166 SBT Toán 9 Tập 2
Bài tập 15 trang 166 SBT Toán 9 Tập 2
Bài tập 16 trang 167 SBT Toán 9 Tập 2
Bài tập 17 trang 167 SBT Toán 9 Tập 2
Bài tập 18 trang 167 SBT Toán 9 Tập 2
Bài tập 19 trang 167 SBT Toán 6 Tập 1
Bài tập 20 trang 168 SBT Toán 9 Tập 2
Bài tập 21 trang 168 SBT Toán 9 Tập 2
Bài tập 22 trang 168 SBT Toán 9 Tập 2
Bài tập 23 trang 168 SBT Toán 9 Tập 2
Bài tập 24 trang 169 SBT Toán 9 Tập 2
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





