Luyện tập 2 trang 53 SGK Toán 8 Tập 2 Cánh diều - CD

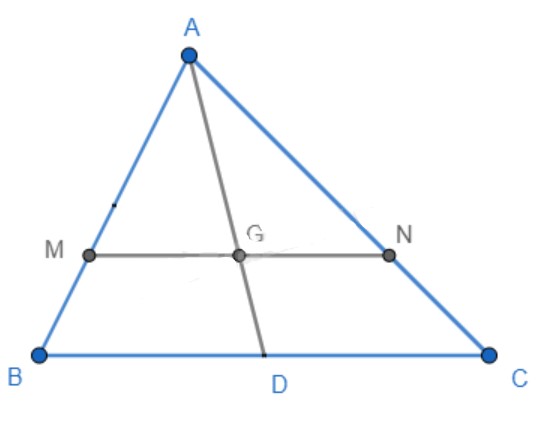
Gọi AD là đường trung tuyến của tam giác ABC (D \(\in\) BC).

Vì G là trọng tâm của tam giác ABC nên AG = \(\frac{2}{3}\) AD hay \(\frac{AG}{AD} =\frac{2}{3}\).

Xét tam giác ABD với MG // BD, ta có:

\( \frac {AM}{AB} = \frac{AG}{AD} =\frac{2}{3}\) (Định lí Thales) (1)

Tương tự, xét tam giác ADC với GN // DC, ta có:

\( \frac {AN}{AC} = \frac{AG}{AD} =\frac{2}{3}\) (Định lí Thales) (2)

Từ (1) và (2) suy ra \( \frac{AM}{AB} = \frac{AN}{AC} = \frac{2}{3} \) (đpcm).

-- Mod Toán 8 HỌC247