Bài tập 40 trang 84 SBT Toán 8 Tập 1

Hướng dẫn giải

Sử dụng định nghĩa, tính chất đường trung bình của tam giác và hình thang:

+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

+) Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.

+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Lời giải chi tiết

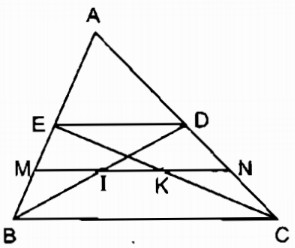
Trong tam giác \(ABC\) ta có:

\(E\) là trung điểm của cạnh \(AB\)

\(D\) là trung điểm của cạnh \(AC\)

Nên \(ED\) là đường trung bình của \(∆ ABC\)

\( \Rightarrow ED//BC\) và \(ED = \displaystyle {1 \over 2}BC\) (tính chất đường trung bình của tam giác)

Vì \(ED//BC\) nên tứ giác \(BCDE\) là hình thang. 

Trong hình thang \(BCDE,\) ta có: \(BC // DE\)

\(M\) là trung điểm cạnh bên \(BE\)

\(N\) là trung điểm cạnh bên \(CD\)

Nên \(MN\) là đường trung bình hình thang \(BCDE ⇒ MN // DE\)

\(MN =\displaystyle  {{DE + BC} \over 2}\)\( = \displaystyle { \displaystyle {{\displaystyle {BC} \over 2} + BC} \over 2} = {{3BC} \over 4}\) (tính chất đường trung bình hình thang)

Trong tam giác \(BED\) ta có:

\(M\) là trung điểm của \(BE\)

\(MI // DE\)

Suy ra: \(MI\) là đường trung bình của \(∆ BED\)

\( \Rightarrow MI = \displaystyle  {1 \over 2}DE \)\(= \displaystyle {1 \over 2}.{1 \over 2}BC= {1 \over 4}BC\) (tính chất đường trung bình tam giác)

Trong tam giác \(CED\) ta có:

\(N\) là trung điểm của \(CD\)

\(NK // DE\)

Suy ra: \(NK\) là đường trung bình của \(∆ CED\)

\( \Rightarrow NK = \displaystyle {1 \over 2}DE \)\( =\displaystyle {1 \over 2}.{1 \over 2}BC= {1 \over 4}BC\) (tính chất đường trung bình tam giác)

\(\eqalign{
& IK = MN - \left( {MI + NK} \right) \cr 
& = {3 \over 4}BC - \left( {{1 \over 4}BC + {1 \over 4}BC} \right) = {1 \over 4}BC \cr 
& \Rightarrow MI = IK = KN = {1 \over 4}BC \cr} \)

-- Mod Toán 8 HỌC247