Bài tập 4.5 trang 48 SBT Toán 8 Tập 1 Kết nối tri thức
Cho hình ABCD (AB // DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC, BC theo thứ tự tại M, I, N. Chứng minh rằng:
a)
b)
Hướng dẫn giải chi tiết Bài tập 4.5
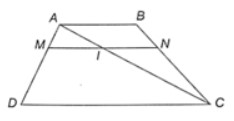
a) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: .
Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: .
Từ đó, suy ra .
b) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: .
Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: .
Khi đó .
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


