Bài tập 3.4 trang 32 SBT Toán 8 Tập 1 Kết nối tri thức
Tìm điểm M bên trong tứ giác ABCD sao cho tổng khoảng cách từ M đến bốn đỉnh A, B, C, D là bé nhất?
Hướng dẫn giải chi tiết Bài tập 3.4
– Trước hết cho hai điểm phân biệt P, Q thì với mọi điểm M ta có MP + MQ ≥ PQ và MP + MQ = PQ chỉ khi M thuộc đoạn thẳng PQ.
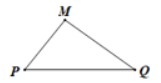
Thật vậy, nếu M không thuộc đường thẳng PQ thì MP + MQ > PQ (bất đẳng thức tam giác) (hình vẽ)
Nếu M thuộc đoạn thẳng PQ thì MP + MQ = PQ (hình vẽ)
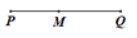
Nếu M thuộc đường thẳng PQ nhưng không thuộc đoạn thẳng PQ thì hoặc P nằm giữa M và Q hoặc Q nằm giữa P và M, dễ thấy trong cả hai trường hợp đó, MP + MQ > PQ (hình vẽ).
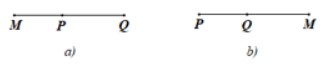
– Xét điểm M tuỳ ý trong tứ giác ABCD (hình vẽ).
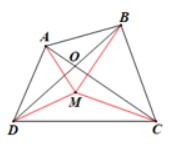
Ta có: MA + MC ≥ AC và MA + MC = AC khi điểm M nằm trên đoạn thẳng AC.
MB + MD ≥ BD và MB + MD = BD khi điểm M nằm trên đoạn thẳng BD.
Do đó MA + MB + MC + MD ≥ AC + BD và MA + MB + MC + MD = AC + BD chỉ khi M vừa thuộc đoạn thẳng AC vừa thuộc đoạn thẳng BD tức là M phải trùng với giao điểm O của AC và BD.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.



