Giải bài 5 trang 63 SBT Toán 7 Chân trời sáng tạo tập 1
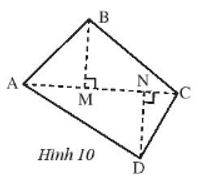
Tính thể tích của một hình lăng trụ đứng đáy là một tứ giác như Hình 10, có độ dài AC = 5 m, BM = DN = 3 m, chiều cao của lăng trụ 7 m.
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
Ta chia tứ giác thành 2 tam giác rồi tính lần lượt diện tích từng tam giác, cộng hai diện tích tam giác đó ta được diện tích đáy rồi suy ra thể tích hình lăng trụ qua công thức V = Sđ . h
Lời giải chi tiết
Từ Hình 10, ta thấy đáy của hình lăng trụ là một tứ giác, ta chia tứ giác đó thành 2 tam giác.
Tam giác ABC có chiều cao BM = 3 m và cạnh đáy AC = 5 m, diện tích tam giác ABC là:
SABC = \(\dfrac{1}{2}\). BM . AC = \(\dfrac{1}{2}\) . 3 . 5 = \(\dfrac{{15}}{2}\) (m2).
Tam giác ADC có chiều cao DN = 3 m và cạnh đáy AC = 5 m, diện tích tam giác ADC là:
SADC = \(\dfrac{1}{2}\) . DN . AC = \(\dfrac{1}{2}\) . 3 . 5 = \(\dfrac{{15}}{2}\) (m2).
Diện tích đáy của hình lăng trụ đã cho là: Sđ = SABC + SADC = \(\dfrac{{15}}{2}\)+ \(\dfrac{{15}}{2}\) = 15 (m2).
Thể tích của hình lăng trụ là: V = Sđ . h = 15 . 7 = 105 (m3).
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 3 trang 63 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 63 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 63 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 64 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 64 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.