Giải bài 2 trang 62 SGK Toán 7 Chân trời sáng tạo tập 2
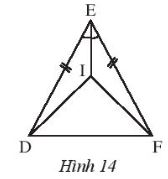
Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)
Chứng minh rằng:
a) \(\Delta EID = \Delta EIF\)
b) Tam giác DIF cân
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
- Ta sử dụng tính chất c-g-c để chứng minh câu a
- Từ câu a ta suy ra ID = FI và chứng minh được tam giác DIF cân
Lời giải chi tiết
a) Xét tam giác EID và tam giác EIF có :
IE chung
ED = EF
\(\widehat {IED} = \widehat {IEF}\)( EI là tia phân giác của \(\widehat {DEF}\))
\( \Rightarrow \Delta EID = \Delta EIF(c - g - c)\)
b) Vì \(\Delta EID = \Delta EIF\) nên ID = IF ( 2 cạnh tương ứng )
Do đó tam giác DIF cân tại I (theo định nghĩa tam giác cân)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Vận dụng 2 trang 62 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 62 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 63 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 63 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 63 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 63 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 49 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 49 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 49 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 49 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 49 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 50 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.