Thực hành 5 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST

Phương pháp giải:

Dựng đường cao và sử dụng định lí Pitago.

Lời giải chi tiết:

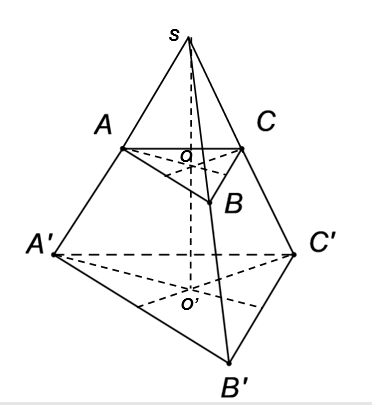
Gọi \(O,O'\) lần lượt là tâm của hai đáy \(ABC\) và \(A'B'C'\), \(M,M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\).

Kẻ \(A'H \bot AO\left( {H \in AO} \right) \Rightarrow A'H = OO'\)

\(\Delta ABC\) đều \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)

\(\Delta A'B'C'\) đều \( \Rightarrow A'M' = \frac{{\frac{a}{2}.\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4} \Rightarrow A'O' = \frac{2}{3}A'M' = \frac{{a\sqrt 3 }}{6}\)

\(A'HOO'\) là hình chữ nhật \( \Rightarrow OH = A'O' = \frac{{a\sqrt 3 }}{6}\)

\( \Rightarrow AH = AO - OH = \frac{{a\sqrt 3 }}{6}\)

Tam giác \(AA'H\) vuông tại \(H\)

\( \Rightarrow OO' = A'H = \sqrt {AA{'^2} - A{H^2}} = \frac{{a\sqrt {141} }}{6}\)

-- Mod Toán 11 HỌC247