Bài tập 3 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST

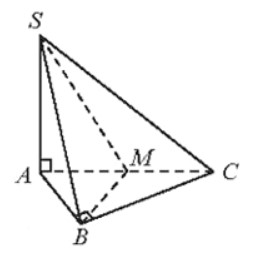
a) Ta có: BC ⊥ AB (giả thiết).

Đồng thời BC ⊥ SA (vì SA ⊥ (ABC)).

$\Rightarrow$ BC ⊥ (SAB)

$\Rightarrow$ (SBC) ⊥ (SAB).

b) Vì tam giác ABC là tam giác vuông cân tại B nên BM ⊥ AC.

Mà BM ⊥ SA (vì SA ⊥ (ABC)).

$\Rightarrow$ BM ⊥ (SAC) (1)

BM $\subset$ (SBM) (2)

Từ (1) và (2) suy ra (SBM) ⊥ (SAC).

-- Mod Toán 11 HỌC247