Hoạt động khám phá 6 trang 63 SGK Toán 11 Chân trời sáng tạo tập 2
Cho đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\) và \(b\) là đường thẳng không thuộc \(\left( P \right)\) và không vuông góc với \(\left( P \right)\). Lấy hai điểm \(A,B\) trên \(b\) và gọi \(A',B'\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( P \right)\).
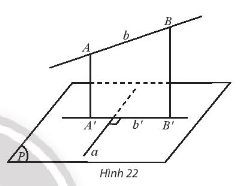
a) Xác định hình chiếu \(b'\) của \(b\) trên \(\left( P \right)\).
b) Cho \(a\) vuông góc với \(b\), nêu nhận xét về vị trí tương đối giữa:
i) đường thẳng \(a\) và \(mp\left( {b,b'} \right)\);
ii) hai đường thẳng \(a\) và \(b'\).
c) Cho \(a\) vuông góc với \(b'\), nêu nhận xét về vị trí tương đối giữa:
i) đường thẳng \(a\) và \(mp\left( {b,b'} \right)\);
ii) giữa hai đường thẳng \(a\) và \(b\).
Hướng dẫn giải chi tiết Hoạt động khám phá 6
Phương pháp giải:
Sử dụng định lí: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
Lời giải chi tiết:
a) Ta có: \(AA' \bot \left( P \right),BB' \bot \left( P \right),A,B \in b\)
Vậy hình chiếu vuông góc của đường thẳng \(b\) trên mặt phẳng \(\left( P \right)\) là đường thẳng \(A'B'\).
Vậy \(b' \equiv A'B'\).
b) Ta có:
\(\left. \begin{array}{l}AA' \bot \left( P \right) \Rightarrow AA' \bot a\\a \bot b\end{array} \right\} \Rightarrow a \bot mp\left( {b,b'} \right)\)
\(\left. \begin{array}{l}a \bot mp\left( {b,b'} \right)\\b' \subset mp\left( {b,b'} \right)\end{array} \right\} \Rightarrow a \bot b'\)
c) Ta có:
\(\left. \begin{array}{l}AA' \bot \left( P \right) \Rightarrow AA' \bot a\\a \bot b'\end{array} \right\} \Rightarrow a \bot mp\left( {b,b'} \right)\)
\(\left. \begin{array}{l}a \bot mp\left( {b,b'} \right)\\b \subset mp\left( {b,b'} \right)\end{array} \right\} \Rightarrow a \bot b\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Hoạt động khám phá 5 trang 62 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 63 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 3 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


