Giải Bài 5 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2

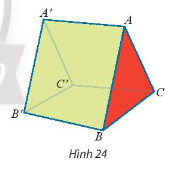
Một cái lều có dạng hình lăng trụ \(ABC.A'B'C'\) có cạnh bên \(AA'\)vuông góc với đáy (Hình 24). Cho biết \(AB = AC = 2,4m;BC = 2{\rm{ }}m;AA' = 3m\).

a) Tính góc giữa hai đường thẳng \(AA'\) và \(BC\); \(A'B'\) và \(AC\).

b) Tính diện tích hình chiếu vuông góc của tam giác \(ABB'\) trên mặt phẳng \(\left( {BB'C'C} \right)\).

QUẢNG CÁO

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

b) Sử dụng phép chiếu vuông góc.

Lời giải chi tiết

a) Ta có: \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot BC \Rightarrow \left( {AA',BC} \right) = {90^ \circ }\)

\(A'B'\parallel AB \Rightarrow \left( {A'B',AC} \right) = \left( {AB,AC} \right) = \widehat {BAC}\)

Xét tam giác \(ABC\) có:

\(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{47}}{{72}} \Rightarrow \widehat {BAC} \approx {49^ \circ }15'\)

Vậy \(\left( {A'B',AC} \right) \approx {49^ \circ }15'\).

b) Gọi \(I\) là trung điểm của \(BC\)

Tam giác \(ABC\) cân tại \(A \Rightarrow AI \bot BC\)

\(\left. \begin{array}{l}AA' \bot \left( {ABC} \right)\\BB'\parallel AA'\end{array} \right\} \Rightarrow BB' \bot \left( {ABC} \right) \Rightarrow BB' \bot AI\)

\( \Rightarrow AI \bot \left( {BB'C'C} \right)\)

\( \Rightarrow I\) là hình chiếu vuông góc của \(A\) trên mặt phẳng \(\left( {BB'C'C} \right)\)

Có \(B,B' \in \left( {BB'C'C} \right)\)

Vậy \(\Delta IBB'\) là hình chiếu vuông góc của \(\Delta ABB'\) trên mặt phẳng \(\left( {BB'C'C} \right)\)

Ta có: \(BB' = AA' = 3,BI = \frac{1}{2}BC = 1 \Rightarrow {S_{\Delta IBB'}} = \frac{1}{2}BB'.BI = 1,5\left( {{m^2}} \right)\)

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Giải Bài 5 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST HAY thì click chia sẻ