Bài tập 4 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST

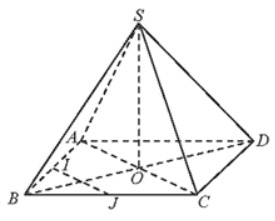
a) Từ giả thiết, dễ dàng nhận thấy ∆SAC và ∆SBD là các tam giác cân.

Ta có: \(\left\{ \begin{matrix} SO\bot AC \\ SO\bot BD \\ \end{matrix} \right.\)

Do đó SO ⊥ (ABCD).

b) Ta có AC ⊥ BD và AC ⊥ SO, suy ra AC ⊥ (SBD).

IJ là đường trung bình của ∆ABC nên IJ // AC.

Do đó IJ ⊥ (SBD).

c) Ta có BD ⊥ AC (ABCD là hình thoi) và BD ⊥ SO, suy ra BD ⊥ (SAC).

-- Mod Toán 11 HỌC247