Giải Bài 9.5 trang 86 SGK Toán 11 Kết nối tri thức tập 2
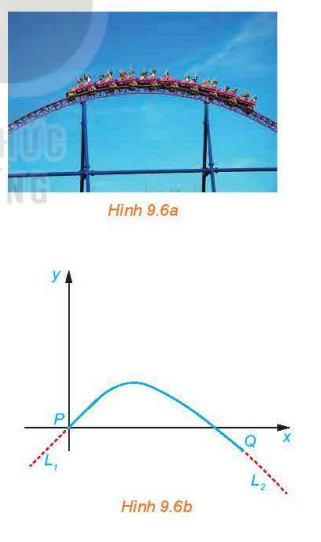
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên \(L_{1}\), và đoạn dốc xuống \(L_{2}\), là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, \(L_{1}\) và \(L_{2}\) phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc toạ độ đặt tại P và phương trình của parabol là \(y = ax^{2} + bx + c\), trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.
d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.
Hướng dẫn giải chi tiết Bài 9.5
Phương pháp giải
Sử dụng phương trình tiếp tuyến của đồ thị hàm số tại điểm P(xo,yo) là
y - yo = f' (xo)( x − xo ),
trong đó yo = f(xo).
Lời giải chi tiết
a) Ta có
\(y' = 2ax + b\)
Ta lại có phương trình của tiếp tuyến là:
\(y-y_{p}=y'(x_{p})(x-x_{p})\)
Thay các giá trị này vào phương trình tiếp tuyến, ta có:
\(0=2ap+b\)
Vậy \(b=-2ap\) thay x=0 vào phương trình đường cong ta có
\(y=a(0)^{2}+c(0)+c=c \Rightarrow c=yp\)
b) \(y'=2ax+b=c\) khi \(x=0\Rightarrow y'(0)b\)
c) Ta có
\(y'(P)=2aP+b=0,5\)
\(y'(P)=2aP+b=0,75\)
Trừ hai phương trình, ta có:
\(2a(Q-P)=-1,25\)
\(Q-P=20\)
\(\Rightarrow a=\frac{-1,25}{40}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Giải Bài 9.3 trang 86 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.4 trang 86 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 9.1 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.2 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.3 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.4 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.5 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.6 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.7 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





