Hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 2 Bài 1 Dãy số môn Toán lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khởi động trang 45 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Gọi u1; u2; u3; ...; un lần lượt là diện tích các hình vuông có độ dài cạnh là 1; 2; 3; ...; n. Tính u3 và u4.
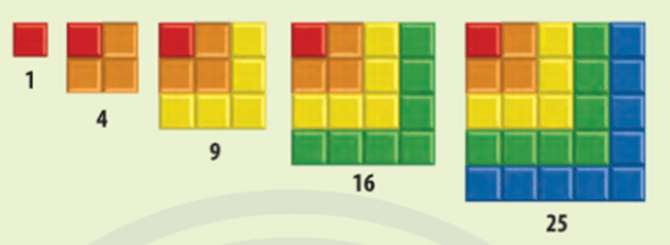
-
Hoạt động khám phá 1 trang 45 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
\(u:{\mathbb{N}^*} \to \mathbb{R}\)
\(n \mapsto {u(n)} = {n^2}\)
Tính \(u\left( 1 \right);u\left( 2 \right);u\left( {50} \right);u\left( {100} \right)\).
-
Hoạt động khám phá 2 trang 46 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hàm số:
\(v:\left\{ {1;2;3;4;5} \right\} \to \mathbb{R}\)
\(n \to {\rm{ }}v\left( n \right) = 2n\)
Tính \(v\left( 1 \right),v\left( 2 \right),v\left( 3 \right),v\left( 4 \right),v\left( 5 \right)\).
-
Thực hành 1 trang 46 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số:
\(u:{\mathbb{N}^*} \to \mathbb{R}\)
\(n \mapsto {u_n} = {n^3}\)
a) Hãy cho biết dãy số trên là hữu hạn hay vô hạn.
b) Viết năm số hạng đầu tiên của dãy số đã cho.
- VIDEOYOMEDIA
-
Vận dụng 1 trang 46 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho 5 hình tròn theo thứ tự có bán kính 1; 2; 3; 4; 5.
a) Viết dãy số chỉ diện tích của 5 hình tròn này.
b) Tìm số hạng đầu và số hạng cuối của dãy số trên.
-
Hoạt động khám phá 3 trang 46 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho các dãy số \(\left( {{a_n}} \right),\left( {{b_n}} \right),\left( {{c_n}} \right),\left( {{d_n}} \right)\) được xác định như sau.
• \({a_1} = 0;{a_2} = 1;{a_3} = 2;{a_4} = 3;{a_5} = 4\).
• \({b_n} = 2n\).
• \(\left\{ \begin{array}{l}{c_1} = 1\\{c_n} = {c_{n - 1}} + 1\left( {n \ge 2} \right)\end{array} \right.\).
• \({d_n}\) là chu vi của đường tròn có bán kính \(n\).
Tìm bốn số hạng đầu tiên của các dãy số trên.
-
Thực hành 2 trang 47 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi: \(\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = 2{u_n}\left( {n \ge 1} \right)\end{array} \right.\).
a) Chứng minh \({u_2} = 2.3;{u_3} = {2^2}.3;{u_4} = {2^3}.3\).
b) Dự đoán công thức số hạng tổng quát của dãy số \(\left( {{u_n}} \right)\).
-
Vận dụng 2 trang 47 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1 cột gỗ (Hình 1). Gọi \({u_n}\) là số cột gỗ nằm ở lớp thứ 2 tính từ trên xuống và cho biết lớp trên cùng có 14 cột gỗ. Hãy xác định dãy số \(\left( {{u_n}} \right)\) bằng hai cách:
a) Viết công thức số hạng tổng quát \({u_n}\).
b) Viết hệ thức truy hồi.

-
Hoạt động khám phá 4 trang 48 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho hai dãy số \(\left( {{a_n}} \right)\) và \(\left( {{b_n}} \right)\) được xác định như sau: \({a_n} = 3n + 1;\) \({b_n} = - 5n\).
a) So sánh \({a_n}\) và \({a_{n + 1}},\forall n \in {\mathbb{N}^*}\).
b) So sánh \({b_n}\) và \({b_{n + 1}},\forall n \in {\mathbb{N}^*}\).
-
Thực hành 3 trang 48 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Xét tính tăng, giảm của các dãy số sau:
a) \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n - 1}}{{n + 1}}\);
b) \(\left( {{x_n}} \right)\) với \({x_n} = \frac{{n + 2}}{{{4^n}}}\);
c) \(\left( {{t_n}} \right)\) với \({t_n} = {\left( { - 1} \right)^n}.{n^2}\).
-
Vận dụng 3 trang 49 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1 cột gỗ (Hình 1).
a) Gọi \({u_1} = 25\) là số cột gỗ có ở hàng dưới cùng của chồng cột gỗ, \({u_n}\) là số cột gỗ có ở hàng thứ \(n\) tính từ dưới lên trên. Xét tính tăng, giảm của dãy số này.
b) Gọi \({v_1} = 14\) là số cột gỗ có ở hàng trên cùng của chồng cột gỗ, \({v_n}\) là số cột gỗ có ở hàng thứ \(n\) tính từ trên xuống dưới. Xét tính tăng, giảm của dãy số này.

-
Hoạt động khám phá 5 trang 49 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{n}\). So sánh các số hạng của dãy số với 0 và 1.
-
Thực hành 4 trang 49 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Xét tính bị chặn của các dãy số sau:
a) \(\left( {{a_n}} \right)\) với \({a_n} = \cos \frac{\pi }{n}\);
b) \(\left( {{b_n}} \right)\) với \({b_n} = \frac{n}{{n + 1}}\)
-
Giải Bài 1 trang 50 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Tìm \({u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\) của dãy số:
\(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = \frac{{{u_n}}}{{1 + {u_n}}}\left( {n \ge 1} \right)\end{array} \right.\)
-
Giải Bài 2 trang 50 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{n\left( {n + 1} \right)}}\). Tìm \({u_1},{u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\).
-
Giải Bài 3 trang 50 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Xét tính tăng, giảm của dãy số \(\left( {{y_n}} \right)\) với \({y_n} = \sqrt {n + 1} - \sqrt n \).
-
Giải Bài 4 trang 50 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Xét tính bị chặn của các dãy số sau:
a) \(\left( {{a_n}} \right)\) với \({a_n} = {\sin ^2}\frac{{n\pi }}{3} + \cos \frac{{n\pi }}{4}\);
b) \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{6n - 4}}{{n + 2}}\)
-
Giải Bài 5 trang 50 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n - 1}}{{n + 1}}\).
Chứng minh \(\left( {{u_n}} \right)\) là dãy số tăng và bị chặn.
-
Giải Bài 6 trang 50 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{na + 2}}{{n + 1}}\). Tìm giá trị của \(a\) để:
a) \(\left( {{u_n}} \right)\) là dãy số tăng;
b) \(\left( {{u_n}} \right)\) là dãy số giảm.
-
Giải Bài 7 trang 50 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
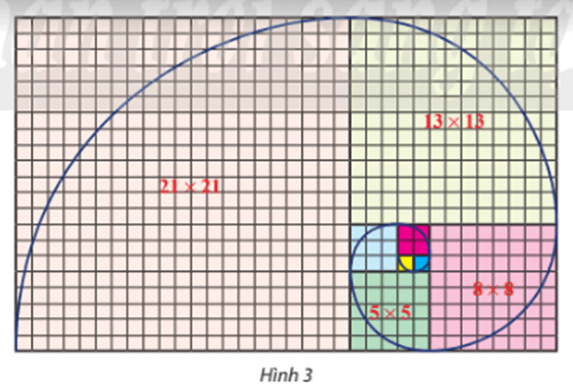
-
Bài tập 1 trang 57 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho dãy số (un) với Số là số hạng thứ bao nhiêu của dãy số?
-
Bài tập 2 trang 57 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Dự đoán công thức số hạng tổng quát của dãy số (un), biết
-
Bài tập 3 trang 57 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Cho dãy số (un) xác định bởi Tìm số hạng thứ năm của dãy số đó?
-
Bài tập 4 trang 57 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Xét tính bị chặn của dãy số (un) với un = (‒1)n?
-
Bài tập 5 trang 58 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Xét tính tăng, giảm và bị chặn của dãy số (un) cho bởi số hạng tổng quát un sau:
a)
b)
c)
-
Bài tập 6 trang 58 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Xét tính tăng, giảm của các dãy số (un) cho bởi số hạng tổng quát un sau:
a)
b)
c)
-
Bài tập 7 trang 58 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Xét tính tăng, giảm và bị chặn của dãy số (\(u_n\)) với ?





