Bài tập 55 trang 221 SGK Toán 11 NC
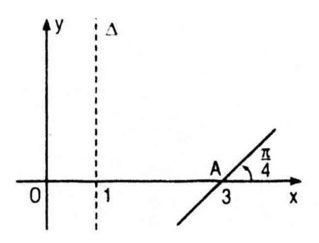
Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).
Hướng dẫn giải chi tiết
Đa thức phải tìm có dạng : P(x) = ax2 + bx + c (a ≠ 0)
Ta có: P′(x) = 2ax + b
Vì trục đối xứng (∆) có phương trình x = 1 nên : \(\frac{{ - b}}{{2a}} = 1\) (1)
Vì đồ thị (P) đi qua điểm A(3 ; 0) nên ta có P(3) = 0, tức là: 9a + 3b + c = 0 (2)
Vì hệ số góc của tiếp tuyến tại điểm A(3 ; 0) bằng \(tan\frac{\pi }{4}\) nên ta có P′(3) = 1, tức là :
6a + b = 1(3)
Giải hệ ba phương trình (1), (2) và (3) với ba ẩn số a, b và c, ta được:
\(\begin{array}{l}
a = \frac{1}{4}\\
b = - \frac{1}{2}\\
c = - \frac{3}{4}
\end{array}\)
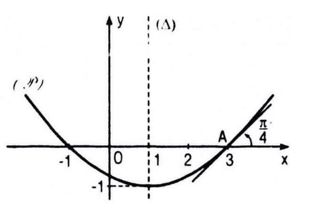
Vậy \(P(x) = \frac{1}{4}{x^2} - \frac{1}{2}x - \frac{3}{4}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 53 trang 221 SGK Toán 11 NC
Bài tập 54 trang 221 SGK Toán 11 NC
Bài tập 56 trang 221 SGK Toán 11 NC
Bài tập 57 trang 222 SGK Toán 11 NC
Bài tập 58 trang 222 SGK Toán 11 NC
Bài tập 59 trang 222 SGK Toán 11 NC
Bài tập 60 trang 222 SGK Toán 11 NC
Bài tập 61 trang 222 SGK Toán 11 NC
-
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = x^3-4x^2+x+1\) tại điểm có hoành độ bằng 1
bởi Nguyễn Thủy Tiên
07/02/2017
Help me!
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = x^3-4x^2+x+1\) tại điểm có hoành độ bằng 1.
Theo dõi (0) 2 Trả lời -
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=x^4+2x^2\) biết tiếp tuyến song song với đường thẳng \(y=8x\)
bởi Chai Chai
08/02/2017
Cứu với mọi người!
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=x^4+2x^2\) biết tiếp tuyến song song với đường thẳng \(y=8x\)
Theo dõi (0) 2 Trả lời -
Viết phương trình tiếp tuyến với đồ thị hàm số \(y=x^3+3x^2-2\), biết rằng tiếp tuyến vuông góc với đường thẳng \(d:x+9y-3=0\)
bởi Mai Thuy
07/02/2017
Cứu với mọi người!
Viết phương trình tiếp tuyến với đồ thị hàm số \(y=x^3+3x^2-2\), biết rằng tiếp tuyến vuông góc với đường thẳng \(d:x+9y-3=0\).
Theo dõi (0) 1 Trả lời -
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{2x+1}{x-2}\) tại điểm có tung độ bằng 3
bởi Anh Nguyễn
08/02/2017
Mình giải ra đáp số rồi mà không biết đúng hay sai nữa, khó quá.
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{2x+1}{x-2}\) tại điểm có tung độ bằng 3
Theo dõi (0) 1 Trả lời -
ADMICRO
Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung
bởi Trần Phương Khanh
08/02/2017
Cho hàm số \(y=x^3-3x^2-3x-2\) có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung.
Theo dõi (0) 1 Trả lời -
Tìm tọa độ điểm M thuộc (C) sao cho tiếp tuyến của (C) tại M tạo với trục tọa độ một tam giác cân.
bởi thi trang
08/02/2017
Cho hàm số \(y=\frac{x}{x+1}\). Tìm tọa độ điểm M thuộc (C) sao cho tiếp tuyến của (C) tại M tạo với trục tọa độ một tam giác cân.
Theo dõi (0) 1 Trả lời -
Tìm giá trị lớn nhất của biểu thức: \(P=\frac{1}{x+y+z+1}-\frac{1}{(1+x)(1+y)(1+z)}\)
bởi Choco Choco
07/02/2017
Với x, y , z \(\geq\) 0, tìm giá trị lớn nhất của biểu thức:
\(P=\frac{1}{x+y+z+1}-\frac{1}{(1+x)(1+y)(1+z)}\)Theo dõi (0) 1 Trả lời
